Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen (Übersicht)
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 - Wissensfragen
a) Falsch, der finally-Block wird immer ausgeführt (abgesehen von einigen extrem konstruierten Ausnahmen, siehe hier)
b) Antwort RO ist richtig: Stark zusammenhängend
c) 2. Antwort ist richtig: Preorder. Postorder müsste auch stimmen, denn die Reihenfolge, ob zuerst nach links oder rechts abgestiegen wird, ist nicht festgelegt.
Doch die Reihenfolge ist festgelegt: L-R-N (Links, Rechts, Mitte), siehe WS 2017/2018 - Folie 12-52 ⇒ nur Preorder ist richtig, so kommt man dann auch am Ende der Aufgabe auf die 10 Antworten = 10 Punkte.
d) Richtig
e) Richtig, beispielsweise wenn sich die Werte für BucketSort eignen
f)
- f ist linear rekursiv
nach Definition ist eine Funktion genau dann linear rekursiv, wenn sie in jedem Zweig einer Fallunterscheidung höchstens einmal aufgerufen wird.
Bei Funktion f gilt:
Fall 1: Ist (x < = 0) ∨ (x % 2 = 0), also für die Zahlen (…, -3, -2, -1, 0, 2, 4, 6, …), kommt es zu gar keinem rekursiven Funktionsaufruf.
Fall 2: Ist (x > 0) ∧ (x % 2 != 0) ∧ (x % 3 != 0), also für die Zahlen (1, 5, 7, 11, 13, …) wird x um eins inkrementiert und der Schleiferumpf erneut ausgeführt.
Da jetzt mit Sicherheit Fall 1 vorliegt, kommt es ebenfalls zu keinem rekursiven Funktionsaufruf.
Fall 3: Ist (x > 0) ∧ (x % 2 != 0) ∧ (x % 3 == 0), also für die Zahlen (3, 9, 15, …), kommt es zu einem rekursiven Aufruf f(x+1). Bei diesem Aufruf liegt mit Sicherheit Fall 1
vor, weshalb x = x + 1 gilt. Anschließend wird x um eins inkrementiert und wir sind garantiert im Fall 2, bei dem es zu keinem rekursiven Funktionsaufruf kommt.
Damit ist gezeigt, dass f linear rekursiv ist.
- g ist iterativ
nach Definition ist eine Funktion f nur genau dann rekursiv, wenn zur Berechnung von f diese Funktion f benutzt wird.
g) Antwort RO und LU sind richtig
h) Falsch, dies ist die grundlegende AVL-Eigenschaft
Aufgabe 2 - Graphen
a)
Adjazenzmatrix
| S | A | B | C | D | E | |
|---|---|---|---|---|---|---|
| S | 0 | 1 | 1 | 0 | 0 | 0 |
| A | 0 | 0 | 0 | 1 | 1 | 0 |
| B | 0 | 0 | 0 | 0 | 1 | 0 |
| C | 0 | 0 | 0 | 0 | 0 | 1 |
| D | 0 | 0 | 0 | 1 | 0 | 1 |
| E | 0 | 0 | 0 | 0 | 0 | 0 |
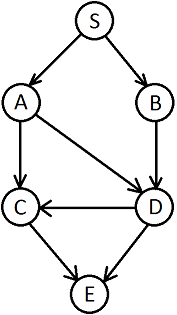
Graphische Darstellung
Als Reihung (eingebettet in Array; auch Adjazenzfeld genannt)
| S | S | A | A | B | C | D | D | |||||||
| S | A | B | C | D | E | A | B | C | D | D | E | C | E | |
| Array-Indizes: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Array-Werte: | 6 | 8 | 10 | 11 | 12 | 14 | 1 | 2 | 3 | 4 | 4 | 5 | 3 | 5 |
|---|
b)
Tiefensuche: S → A → C → E → D → B
Breitensuche: S → A → B → C → D → E
c)
Vorüberlegungen:
Die Aufgabenstellung ist das Färben eines Graphen mit den Farben schwarz und grau. Die Farbe weiß bedeutet lediglich, dass dieser Knoten noch gar nicht gefärbt wurde.
Bei dem Verfahren soll Breitensuche verwendet werden.
Elementare Erkenntnis hierbei:
Hat ein Knoten zwei (oder mehr) Nachbarn, die verschiedene Farben haben, so kann der aktuelle Knoten nicht gefärbt werden, ohne dass er die gleiche Farbe wie mindestens ein Nachbarknoten erhält.
Das bedeutet: Hat ein Knoten mindestens einen Nachbarn, der grau ist und mindestens einen, der schwarz ist, so lässt sich der Graph nicht färben und das Verfahren soll mit dem Rückgabewert „false“ terminieren.
boolean color(Node v) { LinkedList<Node> q = new LinkedList<Node>(); v.color = BLACK; q.addLast(v); // Solange es noch unbesuchte Knoten gibt while(!q.isEmpty()) { // Aktuellen Knoten aus der Queue entnehmen: // Dieser Knoten ist noch WHITE und soll nun korrekt gefärbt werden Node current = q.removeFirst(); // Variable für die Farbe der Nachbarn, zunächst WHITE (d.h. uninitialisiert) Color neighborColor = WHITE; // Gehe alle Nachbarknoten einmal durch for(Node n : neighbors) { // Ist der aktuelle Nachbar WHITE, dann wurde er noch nicht besucht // -> Füge ihn der Queue hinzu if(n.color == WHITE) { q.addLast(n); // Ist der aktuelle Nachbar nicht WHITE, dann wurde er schon besucht // und ist entweder BLACK oder GRAY } else { // Ist die Variable für die Farbe der Nachbarn noch nicht gesetzt // (d.h. WHITE), dann initialisiere sie anhand des aktuellen Nachbarn if(neighborColor == WHITE) neighborColor = n.color; // Hat der aktuelle Nachbar eine andere Farbe, als die bisher // betrachteten Nachbarknoten, dann ist der Graph nicht färbbar if(n.color != neighborColor) return false; } } // Färbe den Knoten korrekt ein und markiere ihn so als besucht // Die Farbe muss das Gegenteil der Farbe der Nachbarn sein! // Gab es keine Färbung der Nachbar, so wird der Knoten BLACK current.color = (neighborColor == BLACK) ? GRAY : BLACK; } // Die Schlange ist leer, alle Knoten wurden abgearbeitet, der Graph // wurde erfolgreich gefärbt. return true;
Aufgabe 3 - Schreibtischlauf
| ad.a | bd.b | gd.a | be.a | ee.a |
| AA | 12 | AA | 12 | AE |
| ad.f(91) | bd.f(92) | gd.f(93) | be.f(95) | ee.f(96) |
| 23 | 92 | 23 | 95 | CE |
| gd.g(83) | ||||
| FC | ||||
| gd.g(„YC“) | ||||
| GC |
Anmerkungen:
- Immer auf die Bindungstypen achten (statisch versus dynamisch)
- Es kommen grundsätzlich nur die Attribute / Methoden in Frage, die der statische Typ kennt
- Bei überladenen Methoden wird die spezifischte verwendet
Programm zum selber Testen: Walkthrough.java
Aufgabe 4 - Sortieren
a)
private static void versickern(Knoten k) { Knoten groesser = null; if (k.links != null && k.rechts != null) { if (k.links.wert > k.rechts.wert) { groesser = k.links; } else { groesser = k.rechts; } } else if (k.links != null) { // hier ist es wichtig, ein "else if" statt einem if zu verwenden! groesser = k.links; } else if (k.rechts != null) { groesser = k.rechts; } if (groesser == null) { return; } if (k.wert > groesser.wert) { return; // fertig :) } vertausche(k, groesser); versickern(groesser); // normalerweise würde man versickern(k) rekursiv aufrufen, aber die vertausche-Methode tauscht laut Aufgabenstellung nicht die Knoten, sondern nur deren Werte! }
b) Nach dem Postorder-Prinzip:
private static void erzeugeHalde(Knoten k) { if (k.links != null) erzeugeHalde(k.links); if (k.rechts != null) erzeugeHalde(k.rechts); versickern(k); }
c)
public static Knoten inListeSortieren() { // Kann leere Halde nicht sortieren if (wurzel == null) { return null; } // Max-Heap-Eigenschaft herstellen erzeugeHalde(wurzel); // Wurzel entnehmen und zum Kopf unserer Liste machen Knoten kopf = entferneMax(); Knoten schlepp = kopf; // Wiederholt Wurzel entnehmen und an Liste anhängen while (wurzel != null) { schlepp.rechts = entferneMax(); schlepp = schlepp.rechts; } // Kopf unserer Liste zurückgeben return kopf; }
Aufgabe 5 - ADT
a)
Alle Instanzen von Tabelle stellen eine verkettete Liste dar. Der älteste, also letzte Eintrag, dieser Liste ist „leer“ und hat keinen Payload und sein Feld „naechster“ zeigt auf null.
double letzte(String lort) { // Sind wir im letzten Element "leer" der Liste? if(naechster == null) return 0; if(ort.equals(lort)) return wert; return naechster.letzte(lort); }
b)
Die Methode meth summiert offenbar den Wert jedes Elements in der List auf.
OPS: meth: Tabelle -> Double AXS: meth(leer) = 0 meth(in(tab, ort, wert)) = wert + meth(tab)
c)
OPS: filter: Tabelle x String -> Tabelle AXS: filter(leer, ort) = leer filter(in(tab, ort, wert), ort2) = in(filter(tab, ort2), ort, wert) falls equals(ort, ort2) = filter(tab, ort2) sonst
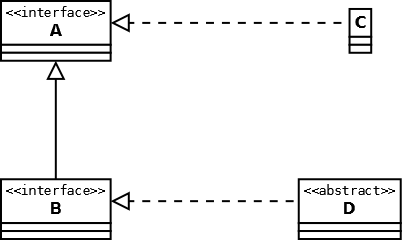
Aufgabe 6 - UML
a)
- 2. Antwort: Komposition
b)
class Buch { protected static int medienZaehler; public String name; private String autor; public Buch(String name, String autor) { } public static int gibMedienZaehler() { } public String gibAutor() { } }
Hinweis:
Konstruktoren haben keinen Rückgabetyp, auch nicht void.
c)
Dia-Sourcefile für etwaige Korrekturen: :pruefungen:bachelor:aud:02-12-uml1.dia.txt
d)
Dia-Sourcefile für etwaige Korrekturen: :pruefungen:bachelor:aud:02-12-uml2.dia.txt
Aufgabe 7 - Formale Verifikation
a)
LO: Falsch i = 1; ret = 1; n ≥ 1 i < n Für n = 1 nicht erfüllt RO: Richtig i = 1; ret = 1; n ≥ 1 ret = Ω_i ∧ i ≤ n Ω_1 = 1 ∧ 1 ≤ n Immer erfüllt! LU: Falsch i = 1; ret = 1; n ≥ 1 ret = Ω_n Offensichtlich nicht für jedes n erfüllt RU: Falsch i = 1; ret = 1; n ≥ 1 indIter(n) = O(n^2) Offensichtlich völliger Quatsch
b)
Zu zeigen: P => I
wp("ret = 1; i = 1;", ret = Ω_i ∧ i ≤ n) =
(1 = Ω_1 ∧ 1 ≤ n) =
(1 = (1 * (2 - 1) * (2 + 1)) / 3 ∧ 1 ≤ n) =
(1 = 3 / 3 ∧ 1 ≤ n) =
(1 ≤ n)
P => I =
(n ≥ 1) => (1 ≤ n) =
(true)
c)
Zu zeigen: {I ∧ ¬b} => wp(A, Q)
Anmerkung: A beschreibt das Programmstück nach der Schleife, aber vor der Nachbedingung. Hier ist A "leer", daher gilt: wp(A, Q) = Q
{I ∧ ¬b} =
(ret = Ω_i ∧ i ≤ n ∧ ¬(i < n)) =
(ret = Ω_i ∧ i ≤ n ∧ i ≥ n) =
(ret = Ω_i ∧ i = n) =
(ret = Ω_n)
{I ∧ ¬b} => wp(A, Q) =
{I ∧ ¬b} => Q =
(ret = Ω_n) => Q =
(ret = Ω_n) => (ret = Ω_n) =
(true)
Folgender Abschnitt ist ein korrekter Beweis für die nicht in der Klausur gestellte Fragestellung:
„Weisen Sie formal mittels wp-Kalkül nach, dass I eine gültige Schleifeninvariante ist.“
Zu zeigen: {I ∧ b} => wp(A, I)
wp(A, I) =
wp("i = i + 1; ret = ret + 4 * i * i - 4 * i + 1;", ret = Ω_i ∧ i ≤ n) =
wp("i = i + 1;", ret + 4 * i * i - 4 * i + 1 = Ω_i ∧ i ≤ n) =
(ret + 4 * (i + 1) * (i + 1) - 4 * (i + 1) + 1 = Ω_(i + 1) ∧ (i + 1) ≤ n) =
(ret + 4 * (i + 1)^2 - 4 * (i + 1) + 1 = Ω_(i + 1) ∧ i ≤ n - 1)
Nebenrechnung:
Ω_(i + 1) =
Σ{from 1 to i + 1} (2k - 1)^2 =
Σ{from 1 to i} (2k - 1)^2 + 2*((i + 1) - 1)^2
Nebenrechnung:
(ret + 4 * (i + 1)^2 - 4 * (i + 1) + 1) =
binomische Formel (über Substituierung von (i + 1) eventuell leichter zu sehen)
(ret + (2*(i + 1) - 1)^2)
Daraus ergibt sich:
= (ret + (2*(i + 1) - 1)^2 = Σ{from 1 to i} (2k - 1)^2 + 2*((i + 1) - 1)^2 ∧ i ≤ n - 1) =
(ret = Σ{from 1 to i} (2k - 1)^2 ∧ i ≤ n - 1)
Und nach einem Blick auf die Definition von Ω_i ergibt sich:
Σ{from 1 to i} (2k - 1)^2 = Ω_i
Damit erhalten wir nun:
= (ret = Ω_i ∧ i ≤ n - 1)
{I ∧ b} => wp(A, I) =
{ret = Ω_i ∧ i ≤ n ∧ i < n} => wp(A, I) =
¬{ret = Ω_i ∧ i ≤ n} ∨ wp(A, I) =
(ret ≠ Ω_i) ∨ (i > n) ∨ wp(A, I) =
(ret ≠ Ω_i) ∨ (i > n) ∨ (ret = Ω_i ∧ i ≤ n - 1)
Sind (ret ≠ Ω_i) und (i > n) beide nicht gültig, dann gilt offensichtlich:
(ret = Ω_i) und (i ≤ n)
Gilt (i ≤ n), dann gilt natürlich auch (i ≤ n - 1)
Damit können wir schlussfolgern:
{I ∧ b} => wp(A, I) = (true)
d)
V = n - i i wird stetig inkrementiert -> (-i) ist damit monoton fallend i = 1, i ≤ n und n ≥ 1 -> n - i ≥ 0
e)
Induktionsanfang:
IA_1 (n = 1): Ω_1 = (1 * (2 - 1) * (2 + 1)) / 3 = 3 / 3 = 1 indRec(1) = 1
Induktionsschritt:
Induktionsvorraussetzung:
IV_(n-1) (n-1): indRec(n-1) = Ω_(n-1) gilt für ein n ≥ 1
Aus dem Programmfragment ist zu entnehmen:
indRec(n) = 4*n*n - 4*n + 1 + indRec(n-1) =
über die obigen Induktionsvoraussetzungen kommt man auf:
= 4*n^2 - 4*n + 1 + Ω_(n-1) =
= (2n - 1)^2 + Ω_(n-1) =
= Ω_(n-1) + (2n - 1)^2 =
= Σ{from 1 to i-1} (2k - 1)^2 + (2n - 1)^2 =
= Σ{from 1 to i} (2k - 1)^2 =
= Ω_(n)
q.e.d.
oder