Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 Wissensfragen
a) 1, 2 und 3
- zu 1)
- ⇒ Endrekursion ist ein Spezialfall der linearen Rekursion. Eine endrekursive Methode kann unmittelbar entrekursiviert werden. (4-37)
- zu 2)
- ⇒ Rumpfrekursive Methode := Endrekursive Methode (http://wwwdh.cs.fau.de/IMMD8/Lectures/Algo1/Skript/6-auf-1/algo1-8-6.pdf)
- ⇒ Zusätzlicher Spreicherbedarf >endrekursiver< Methoden := Speicherbedarf unabhängig von Rekursionstiefe, weil: Die für die aufrufende Methode belegten Speicherbereich abgelegten Werte werden nur noch für die Parameterübergabe an die endständig aufgerufene Methode benötigt. Dieser Speicherbereich kann wiederverwendet werden. (F 4-45)
- zu 3)
- ⇒ Eine Methodendeklaration f(x) {…} heißt rekursive Methodendefinition, gdw. f im Block {…} aufgerufen wird. Variante (verschränkte Rekursion):
- im Rumpf von f steht der Aufruf einer Methode g,
- im Rumpf von g steht ein Aufruf der Methode f
- ⇒ f ist dann zwar rekursiv, hat aber keine rekursive Methodendefinition
- zu 4)
- Warum sollte der Speicherbedarf unabhängig der Höhe sein?
b) 2 und 3
- zu 1)
- Überprüfte Ausnahmen := (engl. checked exceptions) Alle Ausnahmeklassen, die von der Klasse Exception mit Ausnahme von RuntimeException und deren Unterklassen abgeleitet sind.
- Pflicht, solche Ausnahmen zu behandeln oder weiterzugeben. Sonst Fehler bei der Übersetzung.
c) 1 und 2
- zu 1)
- O(1) → Länge ermitteln des alten Arrays, neues Array erstellen mit länge +1,
- O(n) → Alle Elemente im alten ablaufen und gleichzeitig ins neue Array kopieren
- zu 2)
- Liste wird länger, wenn ein neues Element angefügt wird. Das kann man vorn mit O(1) machen.
- zu 3)
- doch, wenn der„rechtmäßigen“ Tabelleneintrag eines Schlüsselwerts bereits durch ein „Überlaufelement“ besetzt ist und der Schlüsselwert auf die nächste freie Positon gesetzt werden muss.
- zu 4)
- O ( n ), egal ob Liste oder Array, wenn sortiert. Ansonsten bei verketteten Listen O(n^2);
d) 1 und 4
- zu 2)
- Wenn der Binärbaum aus einem Knoten besteht, dann schon.
- zu 3)
- Grad ist differenziert zu betrachten hinsichtlich „gerichtete“ und „ungerichtete“ Graphen.
- Ungerichtete Graphen ist der Grad die Anzahl an Knoten, mit den ein Knoten direkt in Verbindung steht.
- Gerichtete Graphen haben Eingangs- und Ausgangsknoten, wobei der Eingangsknoten die Anzahl der Elternknoten repräsentiert.
- zu 4)
- Für eine Grobe Abschätzung (F 13-41) trifft dies zu, weil reheap O(log n) n-Mal aufgerufen wird
- Für eine genauere Abschätzung soll der Aufwand in O( n ) liegen. Weil die Höhe der halde viel kleiner als log n ist. Allgemein gibt es ceil( n / 2^(h+1) ) Knoten der Höhe h , wobei rehap für jeden dieser Knoten den Aufwand O(h) hat.
e) 1 und 3
- zu 1)
- zu 2)
- z.B. HeapSort
- zu 3)
- „Ein Sortierverfahren heißt stabil, wenn gleiche Werte ihre relative Reihenfolge nicht ändern.“ (F 13-8)
- zu 4)
- internes Sortierverfahren:
- Alle Datensätze können gleichzeitig im Hauptspeicher gehalten werden.
- Direkter Zugriff auf alle Elemente ist möglich und erforderlich.
- externes Sortierverfahren:
- Sortieren von Massendaten, die auf externen Speichermedien gehalten werden.
- - Zugriff ist auf einen Ausschnitt der Datenelemente beschränkt.
f) 3 und 4
- zu 1)
- Die Länge l des Pfades ist die Anzahl der Kanten im Pfad, also l=n-1
- zu 2)
- doch, wenn es einen Pfad von w nach v gibt.
- zu 3)
- genau die Definition in (F 14-12)
- zu 4)
- Ja, in einem Zyklus können alle Kanten verschieden sein
g) 1 und 4
- zu 1)
- Definition für gerichtete Graphen F 14-17
- zu 2)
- Wurzel ist ein Knoten mit Eingangsgrad 0, bzw, wenn es keine gerichteten Kanten auf ihn gibt.
- zu 3)
- DFS kann kaskadenartig rekursiv und auch iterativ mit expliziten Stack implementiert werden.
- zu 4)
- Ein Graph ist induzierter Teilgraph von G, wenn alle seine Knoten eine Teilmenge der Knoten von G sind und wenn seine Kanten auch in G existieren.
h) 2 und 4
- zu 1)
- this kann nicht in einem statischen Kontext verwendet werden, sonst Fehler ⇒ Cannot use this in a static context
- zu 2)
- ein Konstruktor instanziert ein Objekt der Klasse. Wenn eine Returnanweisung „ return; “ enthalten ist, muss sie leer sein. Verwendung z.B. um eine innerhalb eines Schleifendurchlauf im Konstruktor den Konstruktor komplett zu verlassen.
- zu 3)
- falsch, siehe Externer Link
- zu 4)
- Genau genommen initialisiert die Laufzeitumgebung jede Objekt- und Klassenvariable zunächst mit 0, null oder false und später mit einem Wert. Daher ist die Nullung von Hand nicht nötig: genau das sagt die Antwort, also richtig
Aufgabe 2 Bäume
a)
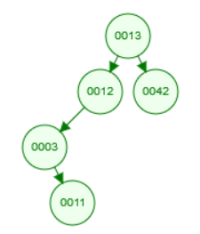
b)
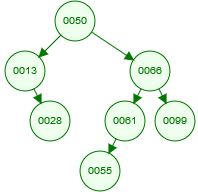
c)

d)

e)
Darstellung als Array: 28,24,13,21,19,3,7
f)
- i)
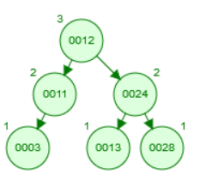
- ii)
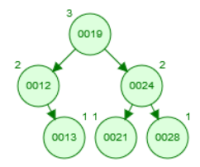
Aufgabe 3 Listen
a)
class Cursor<E> implements ListIterator<E> { private class Node { private E v; // value (payload) private Node p, n; // previous, next } private Node prev, next; public void add(E e) { Node newN = new Node(); // new node becomes next newN.v = e; if(next != null){ next.p=newN; newN.n=next; } if(prev != null){ prev.n=newN; newN.p=prev; } next=newN; }
b)
public E previous() { if(prev != null){ E vTmp=prev.v; next=prev; prev=prev.p; return vTmp; } return null; }
c)
public void remove() { if(next != null){ next=next.n; // interne Verzeigerungen der Liste aktualisieren if(next != null){ next.p = prev; } if(prev != null){ prev.n = next; } } } }
Aufgabe 4 Graphen
a) (E, C), (C, B), (C, D), (D, A)
b)
- Prim: O(e+v*log(v))
- Kruskal: O(e * log(e))
c)
public void floidify(double[][] g){ int n = g.length; for(int i = 0; i < n; i++){ for(int j = 0; j < n; j++){ for(int k = 0; k < n; k++){ if(i != j && i != k && k != j){ // so sehen wir uns garantiert 3 paarweise versch Knoten an if(g[j][i] > 0 && g[i][k] > 0){ // es gibt eine Verbindung von Vj ueber Vi nach Vk if(g[j][k] == 0 || g[j][i]+g[i][k] < g[j][k]){ // bisherige Verbingung zwischen Vj und Vk gab es nicht oder kostet mehr als über Vi -> ersetze alte Verbindung durch neue g[j][k] = g[j][i]+g[i][k]; } } } } } } }
Aufgabe 5 ADT
a)
getCol(Step(l), x, y) = NOT(getCol(l,x,y), falls x = getX(l) && y = getY(l) getCol(Step(l), x, y) = getCol(l,x,y), sonst
b)
getDir(Step(l)) = (getDir(l) + 3) % 4, falls getCol(l, getX(l), getY(l)) == false getDir(Step(l)) = (getDir(l) + 1) % 4, sonst
c)
getX(Step(l)) = getX(l) + 1, falls getDir(Step(l)) == 1 // + und - vertauscht? 1 = Westen, also nach links also -1 getX(Step(l)) = getX(l) - 1, falls getDir(Step(l)) == 3 //wie oben nur umgekehrt, auch in den Bildern zu sehen getX(Step(l)) = getX(l), sonst
d)
Beachte: Das Koordinatensystem ist nach unten geklappt, d.h. die y-Werte drehen sich bei den Blickrichtungen Norden/Sueden um. Wo steht das? Reine Interpretationssache. Das Raster im Bild ist nach oben auch positiv... ---------> x | | | y
public class LangtonAntJava{ boolean[][] raster = new boolean[4711][4242]; int x = 666, y = 666, d = 0; // Position und Richtung void step(){ if(raster[x][y]){ d = (d+1)%4; } else { d = (d+3)%4; } raster[x][y] = !raster[x][y]; if(d == 0){ y -= 1; } else if (d == 1){ x += 1; // muesste hier nicht x -= 1 stehen, da Blickrichtung nach Osten? Stimme dem zu. Autor kennt, wie bei c) schon erwähnt, die Himmelsrichtungen nicht. } else if (d == 2){ y += 1; } else if (d == 3){ x -= 1; // muesste hier nicht x += 1 stehen, da Blickrichtung nach Westen? } } }
Aufgabe 6 Binäre Suche
class BinaereIntervallSuche { Intervall sucheIntervall(Intervall[] is, int v) { int a = 0, m, e = is.length - 1; // Anfang, Mitte, Ende while( e >= a ){ m=(a+e)/2; if(v <= is[m].max && v >= is[m].min) // volltreffer return is[m]; if(v > is[m].max){ // v liegt rechts a=m+1; }else{ // v liegt links e=m-1; } } return null; } }
Aufgabe 7 Backtracking
private static void helfer(int p) { // p durchlaeuft alle Positionen in a // Basisfall a und b (fast) gleich gross erreicht? if (Math.abs(a.size() - b.size()) <= 1) { if (y == null && z == null // erste Loesung benoetigt // oder bessere Loesung gefunden || (Math.abs(abDiff) < Math.abs(yzDiff))) { // merke beste bisher gefundene Loesung: y = new LinkedList<>(a); z = new LinkedList<>(b); yzDiff = abDiff; } } else if (p < a.size()) { // kein Abbruch // Rekursion 1: p-ter Wert bleibt in a: helfer(p + 1); // Rekursion 2: p-ten Wert von a nach b verschieben: abDiff-=2*(a.get(p)); b.add(a.remove(p)); helfer(p); //sollte hier nicht auch p+1 stehen? sonst mach ich den gleichen Schritt nochmal // Nein, da ja der aktuelle Wert der Stelle P entfernt wird, wenn du jetzt p +1 machen würdest, würdest du einen Wert überspringen // Backtracking zur 2. Rekursion: abDiff+=2*b.get(b.size()- 1); a.add(p, b.remove(b.size() - 1)); } }
