Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Lösungsversuch
Inhaltsverzeichnis
Lösungsversuch
1) Wissensfragen
a) 2te, 4te
b) 1te, 2te
c) 2te (O(n log n))
d) 2te, 3te Antwort
e) 1te und 4te
f) 1te, 4te
g) 1te, 4te
h) 1te und 3te
2) Bäume
a)
Linksvollständiger Binärbaum:
S
/ \
U C
/ \
H E
Binärer Suchbaum:
S
/ \
C U
\
H
/
E
(iii) ^
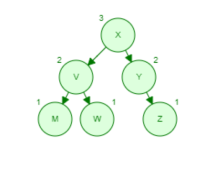
c)
(i) pre-order: E → N → J → H → O → O → D
(ii) in-order: J → N → O → H → E → D → O
(iii) post-order: J → O → H → N → D → O → E
d)
(i) E anstelle von F ??
E
/ \
B G
/ \ \
A C H
\
D
(ii) C anstelle von B ??
A
\
C
\
D
\
E
3) Graphalgorithmen
a)
{A, B, C, D, E}
{A, B, D, E}
{A, B, C, E}
{A, B, C, D}
{F, G, H}
{A, B, C}
{A, B, E}
b)
| A | B | C | D | E |
|---|---|---|---|---|
| ∞ | [0] | ∞ | ∞ | ∞ |
| ∞ | 5B | ∞ | [3B] | |
| 16E | [5B] | 18E | ||
| 14C | [11C] | |||
| [13D] |
Endergebnis: 13 | 0 | 5 | 11 | 3
c)
F –(7)–> B –(5)–> C –(6)–> D –(2)–> A
Weglänge: 7 + 5 + 6 + 2 = 20
4) Backtracking
a)
static boolean exists(boolean[][] brd, int r, int c) { if (brd[r] == null || brd[r].length < 1) { // Zeilen null oder leer return false; } if (r >= brd.length || c >= brd[r].length || r < 0 || c < 0) { // Indizes ausserhalb der Grenzen return false; } return true; }
b)
static int[][] allocateSolutionArray(boolean[][] brd, int mrl) { int[][] = null; int[][] sol = new int[brd.length][mrl]; for (int r = 0; r < brd.length; r++) { for (int c = 0; c < mrl; c++) { if (exists(brd, r, c) && brd[r][c]) { // Diese Felder duerfen betreten werden sol[r][c] = 0; } else { sol[c][c] = -1; // Felder mit -1 vorbelegen } } } return sol; }
c)
static boolean solve(boolean[][] brd, int[][] sol, int tf, int r, int c, int n) { // possible targets from (r,c) int[][] jumps = { { r + 2, c - 1 }, { r + 1, c - 2 }, { r - 1, c - 2 }, { r - 2, c - 1 }, { r - 2, c + 1 }, { r - 1, c + 2 }, { r + 1, c + 2 }, { r + 2, c + 1 } }; //Basisfall, letzter Wert muss hier noch gesetzt werden if (n == tf) { sol[r][c] = n; return true; } for (int j = 0; j < jumps.length; j++) { // Wert setzen sol[r][c] = n // Brett brd und Loesungsfeld sol pruefen if (exists(brd, jumps[j][0], jumps[j][1]) && sol[jumps[j][0]][jumps[j][1]] == 0) { // Rekursion if (solve(brd, sol, tf, jumps[j][0], jumps[j][1], n + 1)) { return true; } // Backtrack sol[r][c] = 0; } } return false; }
Alternative:
a) *
public static boolean exists(boolean[][] brd, int r, int c) { if (r < 0 || c < 0 || r >= brd.length || (brd[r] == null || c >= brd[r].length)) return false; return true; }
b) *
public static int[][] allocateSolutionArray(boolean[][] brd, int mrl) { int[][] sol = null; sol = new int[brd.length][mrl]; for (int y = 0; y < brd.length; y++) { for (int x = 0; x < mrl; x++) { if (x < brd[y].length && !brd[y][x]) { sol[y][x] = -1; } else if (x >= brd[y].length) { sol[y][x] = -1; } } } return sol; }
c) Annahme: P={r, c innerhalb von sol-Array}
public static boolean solve(boolean[][] brd, int[][] sol, int tf, int r, int c, int n) { int[][] jumps = { { r + 2, c - 1 }, { r + 1, c - 2 }, { r - 1, c - 2 }, { r - 2, c - 1 }, { r - 2, c + 1 }, { r - 1, c + 2 }, { r + 1, c + 2 }, { r + 2, c + 1 } }; if (n == tf) { sol[r][c] = n; // Letze Möglichkeit z.B. Start ist einzigste Möglichkeit return true; } for (int[] jump : jumps) { if (exists(brd, jump[0], jump[1]) && sol[jump[0]][jump[1]] == 0) { sol[r][c] = n; if (solve(brd, sol, tf, jump[0], jump[1], n + 1)) { return true; } sol[r][c] = 0; } } return false; }
5) Haldensortierung
a)
Das Element 0 wird im nächsten Schritt versickert. Daher werden die Kindelemente 5 und 2 verglichen. 5 ist größer, daher wird 5 mit 0 verglichen. 5 ist größer, weshalb 5 und 0 getauscht werden.
=> Kreuz bei Stelle 2, 5 und 6
=> Resultat: { 6, 7, 5, 3, 1, 0, 2 }
b)
Ergebnis: { 6, 3, 5, 2, 1, 0, 7 }
c)
void reheap(W[] w, Comparator<W> c, int i, int k) { int leftId = 2 * i + 1; int rightId = leftId + 1; int kidId; // nur 1 Kind (linkes) vorhanden; pruefen, ob Indizes innerhalb des Arrays liegen if (leftId <= k && rightId > k) { if (c.compare(w[leftId], w[i]) > 0) { // Falls Kind groesser, dann tauschen swap(w, leftId, i); } } else { // 2 Kinder vorhanden, pruefen, ob rechtes Kind innerhalb des Arrays liegt if (rightId <= k) { // groesseres der beiden Kinder in kidId speichern kidId = c.compare(w[leftId], w[rightId]) > 0 ? leftId : rightId; // Schauen, ob Kind groesser ist, als aktuelles Element, falls ja, dann tauschen if (c.compare(w[kidId], w[i]) > 0) { swap(w, kidId, i); reheap(w, c, kidId, k); } } } }
d)
void heapSort(W[] w, Comparator<W> c) { int n = w.length; // Phase 1: Halde aufbauen for (int i = n / 2; i >= 0; i--) { reheap(w, c, i, n - 1); } // Phase 2: Maximum entnehmen und sortierte Liste am Ende aufbauen for (int i = n - 1; i > 0; i--) { // Maximum an das Ende der Halde tauschen swap(w, 0, i); // Nach vorne getauschtes Element einsickern lassen und Haldeneigenschaft wiederherstellen reheap(w, c, 0, i - 1); } }
6) Bäume und Rekursion
LinkedList<Node> count(String s) { assert s != null : new IllegalArgumentException(); HashMap<Character, Node> map = new HashMap<>(); for(char c : s.toCharArray()) { Node n = map.get(c); if(n != null) { //variable frequenz updaten n.f++; } else { //neuer node in die map map.put(c, new Node(c,1)); } } return new LinkedList<>(map.values()); } void merge(LinkedList<Node> nodes) { if(nodes.size() > 1) { Collections.sort(nodes); Node zero = nodes.removeFirst(); Node one = nodes.removeFirst(); nodes.addFirst(new Node(zero, one)); merge(nodes); } } String decode(Node root, String b) { assert (root != null && b != null) : new IllegalArgumentException(); return dec(root, root, b); } String dec(Node root, Node node, String b) { if(b.length() < 1 && root != node) { throw new IllegalArgumentException(); } if(b.length() < 1) { return ""; } if(b.charAt(0) == '0') { node = node.zero; } else if(b.charAt(0) == '1') { node = node.one; } else { throw new IllegalArgumentException(); } if(node == null) { throw new IllegalArgumentException(); } if(node.one == null && node.zero == null) { return node.c + dec(root, root, b.substring(1)); } else { return dec(root, node, b.substring(1)); } }