Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 - Wissensfragen
a) Falsch, geschlossenes Hashing bedeutet lediglich, dass es pro Behälter eine Obergrenze b an Schlüsseln gibt. Diese Grenze ist meistens 1, kann aber auch beliebig hoch (jedoch fest!) sein. Für eine fest Obergrenze b ergibt sich allgemein: Die Hashtabelle kann m * b Schlüssel aufnehmen.
b) Falsch, jUnit ist ein TestCase-Framework. Behälterdatentypen werden über das Collections Framework bereitgestellt.
c) 4. Antwort ist richtig: keines davon. Der Entscheidungsgehalt H errechnet sich als: ceil(log_2 (n))
d)
- Passt nicht, die Vererbungsbeziehung fehlt
- Passt
- Passt nicht, die Vererbungsbeziehung geht in die andere Richtung
- Passt nicht, die Methode +byby(a:A) hat keinen Returntyp
- Passt
e) 3. Antwort: n
f) (unsicher)
- 2. Antwort: O(n log(n))
- 3. Antwort: O(m-n)
- 3. Antwort: O(2^abs(n))
Aufgabe 2 - Graphen I
a)
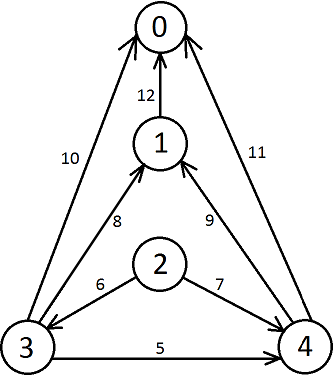
Lösungsweg: Alle Spalten mit einem unendlichen Kantengewicht legen die Knoten fest mit dem Spaltenindex als Knotennamen. In diesem Fall gibt es also die Knoten 0-4 (einschl.). Die Zahlen in der ersten Zeile geben dabei einen Indexbereich im zweiten Teil des Arrays an. Im Folgenden „IK-Zahlen“ genannt.
Der zweite Teil des Arrays ohne unendliche Kantengewichte wird nun also in mehrere Bereiche für jeden Knoten aufgeteilt. Dabei geben die jeweiligen IK-Zahlen die erste Spalte zu einem Bereich an. Für Knoten 0 fängt der Bereich 0 also mit Spalte 5 an. Bereich 1 für Knoten 1 fängt aber auch bei Knoten 5 an, weshalb für Knoten 0 keine Spalte übrig bleibt. Bereich 2 fängt ab Spalte 6 an und damit umfasst Bereich 1 nur Spalte 5. Am Ende sieht unser geteiltes Array also so aus:
Knoten _1__|_______2_______|___________3___________|_______4____
0 | 3 4 | 0 1 4 | 0 1
γ 12 | 6 7 | 10 8 5 | 11 9
Jetzt kann man die Kanten ganz einfach ablesen. Die Kanten gehen dabei immer vom jeweiligen Knoten des Bereiches zu dem Knoten in der ersten Zeile der Tabelle. Somit enstehen aus obiger Tabelle folgende Kanten:
1→0, 2→3, 2→4, 3→0, 3→1, 3→4, 4→0, 4→1
Die zweite Zeile repräsentiert die Kantengewichte.
b)
Ja
c)
Die fehlende Kante: (0 → 2)
Aufgabe 3 - Graphen II
a)
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| [0] | ∞ | ∞ | ∞ | ∞ |
| 0 | 15 | [5] | 9 | ∞ |
| 0 | 14 | 5 | [9] | 13 |
| 0 | [11] | 5 | 9 | 12 |
| 0 | 11 | 5 | 9 | [12] |
| 0 | 11 | 5 | 9 | 12 |
b)
| Vorgänger | Knoten | Nachfolger | (u_j, v_i) + (v_i, w_k) | „alte Länge“ |
|---|---|---|---|---|
| u_j | v_i | w_k | γ_j,i,k | γ_alt |
| 1 | 2 | 5 | 18 | ∞ |
| 3 | 2 | 5 | 12 | 8 |
| 4 | 2 | 5 | 5 | 3 |
| 1 | 3 | 2 | 14 | 15 |
| 1 | 3 | 4 | 15 | 9 |
| 1 | 3 | 5 | 13 | 18 |
| 1 | 4 | 2 | 11 | 14 |
| 1 | 4 | 5 | 12 | 13 |
| 3 | 4 | 2 | 12 | 9 |
| 3 | 4 | 5 | 13 | 8 |
Graph:
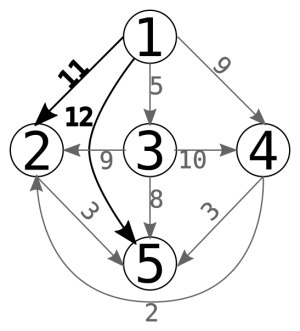
(Allgemeine Bemerkung: Der Algorithmus von Floyd erzeugt jede Kante, die es vorher noch nicht gab, bzw. „verbessert“ die Gewichte von bestehenden Kanten.

Aufgabe 4 - Doppelte binäre Suche
a)
public static int locateRow(int[][] keys, int key) { int start = 0; int end = keys.length - 1; do { int mid = (start + end) / 2; // erster Wert der Zeile ist kleiner oder gleich // => gesuchter Wert kann in der aktuellen Zeile oder in den Zeilen darunter vorkommen if(keys[mid][0] <= key) { // falls die nächste Reihe nicht existiert // => gesuchter Wert kann nur in der aktuellen Zeile sein if(mid + 1 >= keys.length) { return mid; } else { // falls die nächste Reihe existiert, ihr erster Wert aber größer als der gesucht ist // => gesuchter Wert kann nur in der aktuellen Zeile sein if(keys[mid + 1][0] > key) { return mid; } else { start = mid + 1; } } // erster Wert der Zeile ist echt größer // => gesuchter Wert kann nur in den Zeilen darüber vorkommen } else { end = mid - 1; } } while(start <= end && start >= 0 && end <= keys.length); return -1; }
b)
public static int[] search(int[][] keys, int key) { int row = locateRow(keys, key); if(row == -1) return null; int start = 0; int end = keys[row].length - 1; do { int mid = (start + end) / 2; if(keys[row][mid] == key) return new int[]{row, mid}; if(keys[row][mid] < key) { start = mid + 1; } else { end = mid - 1; } } while(start <= end && start >= 0 && end < keys[row].length); return null; }
Programm zum selber Testen: :pruefungen:bachelor:aud:doublebinarysearch.java.txt
Aufgabe 5 - Rekursion
(Hinweis: Sehr komische Aufgabe, eventuell hab ich da auch etwas missverstanden oder falsch interpretiert…)
a)
public GaltonBrett(double p, int faecher) { if(p > 0 && p < 1 && faecher >= 2) { this.p = p; this.baelle = new long[faecher]; } else { throw new IllegalArgumentException(); } }
b)
Die Differenz, wie viel häufiger der Ball nach rechts gefallen ist, als nach links, muss nun auf die Fächer gemappt werden. Problem hierbei ist, dass das Verfahren für ungerade (Fach in der exakten Mitte existiert) und gerade (ein solches Fach existiert nicht) Fächeranzahlen funktionieren muss.
Um sich zu veranschaulichen, warum folgender Code das richtige tut, zeichnet man sich am Besten mal den Fall für 4 Fächer und für 5 Fächer auf und überlegt sich, welche Werte für „diff“ überhaupt möglich sind.
private int berechneFach(int diff) { int mid = baelle.length / 2; if(baelle.length % 2 == 0 && diff < 0) diff--; int fach = mid + (diff / 2); return fach; }
c)
public void simuliere(long n) { for(int i = 0; i < baelle.length; i++) baelle[i] = 0; int ebenen = baelle.length - 1; for(int i = 0; i < n; i++) { int fach = berechneFach(simLinRek(ebenen)); baelle[fach]++; } }
d)
private int simIter(int ebenen) { int diff = 0; while(ebenen > 0) { diff += linksOderRechts(); ebenen--; } return diff; }
Programm zum selber Testen: :pruefungen:bachelor:aud:galtonbrett.java.txt
Aufgabe 6 - Streutabellen
a)
| Bucket | Kollisionsliste |
|---|---|
| 0 | 0 → 8 |
| 1 | |
| 2 | 42 |
| 3 | 11 |
| 4 | |
| 5 | |
| 6 | |
| 7 | 47 → 15 |
b)
| Element | sondierte Buckets |
|---|---|
| 47 | 7 |
| 11 | 3 |
| 0 | 0 |
| 8 | 0 → 3 → 6 |
| 15 | 7 → 2 |
| 42 | 2 → 5 |
Aufgabe 7 - Sortieren
a)
Frage 1:
Ein kürzerer String soll vor einem längeren einsortiert werden, das heißt, bei einem Vergleich muss ein kürzerer String wie ein längerer, jedoch lexikographisch kleinerer String behandelt werden.
Frage 2:
Das Wort muss vorne mit den Füllsymbolen aufgefüllt werden, da die Sortierung von hinten nach vorne erfolgt. Würde man es hinten mit den Füllsymbolen auffüllen, so erreicht man eine lexikographische Sortierung, das heißt:
aal
aligator
com
computer
Die von uns gewünschte Sortierung ist jedoch folgende:
aal
com
aligator
computer
Frage 3:
Ein Vergleichen der Zeichen von hinten nach vorne ist notwendig, damit eine lexikographische Sortierung erfolgt und beispielsweise „aa“ vor „ab“ einsortiert wird. Äußerst wichtig ist hierbei, dass das Verfahren stabil sein muss!
b)
| Stelle | Reihung | |||
|---|---|---|---|---|
| - | /AIA | IPV2 | R2D2 | / /AI |
| 3 | IPV2 | R2D2 | /AIA | / /AI |
| 2 | / /AI | R2D2 | /AIA | IPV2 |
| 1 | / /AI | R2D2 | /AIA | IPV2 |
| 0 | / /AI | /AIA | IPV2 | R2D2 |
c)
Reales Char-Indizes:
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| t | e | s | t |
| a | u | d | |
| a | n | d | |
| s | p | ||
| x |
Virtuelle Char-Indizes (= pos):
| 0 | 1 | 2 | 3 |
|---|---|---|---|
| t | e | s | t |
| a | u | d | |
| a | n | d | |
| s | p | ||
| x |
public static int getBucket(int pos, String name) {
int realPos = pos - (4 - name.length());
if(realPos < 0)
return mapChar('/');
return mapChar(name.charAt(realPos));
}
d)
static void radixSort(ArrayList<String> names) {
List<String>[] b = new ArrayList[37];
for(int bi = 0; bi < b.length; bi++) {
b[bi] = new ArrayList<>();
}
for(int i = 3; i >= 0; i--) {
for(String s : names) {
int bucket = getBucket(i, s);
b[bucket].add(s);
}
names.clear();
for(int bi = 0; bi < b.length; bi++) {
names.addAll(b[bi]);
b[bi].clear();
}
}
}
Programm zum selber Testen: :pruefungen:bachelor:aud:08-12-radixsort.java.txt