Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen (Übersicht)
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 - Wissensfragen
a) E + Unterklassen von E
b) O(|n|)
Begründung:
Nach einmaliger Abarbeitung der inneren Schleife gilt „n == 0“. Dadurch ergibt die Auswertung des Schleifenkopfs der äußeren Schleife „false“ und die Funktion endet.
c) O(n)
Begründung:
Im ersten Durchgang der Schleife werden alle drei Unterfunktionen einmal aufgerufen, das heißt: O(log n) + O(n) + O(1) = O(n) für die erste Iteration.
In allen weiteren Durchläufen wird nur mehr „doSomethingInO(1)“ ausgeführt, das heißt O(1) für alle weiteren Iterationen.
Da es insgesamt n-1 weitere Iterationen gibt, lautet der Gesamtaufwand der weiteren Iterationen O(n)
Insgesamt ergibt sich damit: O(n) + O(n) = O(n)
d) 2. Antwort ist richtig
e) 1. Antwort ist richtig: „Überlädt meth aus C“, da beide Methoden gleich heißen, aber andere Parameter erwarten
f) 2. und 3. Antwort sind richtig
g) false, denn der „==“-Operator vergleicht die Referenzen, nicht den Inhalt der Objekte (das wäre equals())
h) O(log n)
Begründung:
Ein erster Eintrag von Element x lässt sich in einer sortierten Reihung mittels binärer Suche in O(log n) finden.
Um zu prüfen, ob (wie viele ist irrelevant!) es noch weitere Einträge von Element x gibt, muss man nur das Element rechts und links vom aktuellen betrachtet, was in O(1) geht.
Anmerkung: Es geht ja um den worst case. Ich denke, man kann ein Szenario konstruieren, in dem die Laufzeit O(n) beträgt. Wenn z.B. die gesamte Reihung nur aus diesem Element besteht, muss man nach Auffinden des ersten Eintrags, die gesamte Liste durchgehen, um alle Vorkommen zu finden und zu zählen.
i) 2. Antwort ist richtig
j) 3. Antwort ist richtig
Aufgabe 2 - Binärbäume
a)
- Für jeden Knoten gilt: Alle Knoten des linken Teilbaums sind echt kleiner und alle des rechten Teilbaums echt größer sind als der Knoten selbst.
- Mathematisch: ∀ Teilbäume T' des Binärbaums T, T' = (T_l, y, T_r) gilt:
- a) ∀ x ∈ T_l: value(x) < value(y)
- b) ∀ z ∈ T_r: value(z) > value(y)
b)
boolean isSearchTree() { if(left != null) { if(getMax(left.data) >= data || !left.isSearchTree()) return false; } if(right != null) { if(getMin(right) <= data || !right.isSearchTree()) return false; } return true; }
?? oder vielleicht so: ??
boolean isSearchTree() { if (this.left == null && this.right == null) { return true; } else if (this.left == null) { if (this.right.getMin() > this.data) { return this.right.isSearchTree(); } return false; } else if (this.right == null) { if (this.left.getMax() < this.data) { return this.left.isSearchTree(); } return false; } else { if (this.left.getMax() < this.data && this.right.getMin() > this.data) { return this.left.isSearchTree() && this.right.isSearchTree(); } return false; } }
Zum Testen: https://pastebin.com/T6DbJ4iU
c)
- Für jeden Knoten gilt: Der Wert seiner Kinder muss größer als sein eigener Wert sein.
- Mathematisch: Ein partiell geordneter Baum ist ein knotenmarkierter Binärbaum, in dem für jeden Teilbaum T' mit Wurzel x gilt:
- In der Wurzel steht immer das Minimum des Teilbaums, also ∀y ∈ T': value(x) ≤ value(y)
d)
void sanitize() { int smallest = getSmallest(); // aktueller Knoten der kleinste -> fertig if(data == smallest) return; if(left != null && left.data == smallest) { swap(this, left); left.sanitize(); } else { swap(this, right); right.sanitize(); } }
e)
Ein AVL-Baum ist ein binärer Suchbaum, bei dem für jeden Knoten gilt: Die Höhe seiner beiden Teilbäume unterscheidet sich maximal um eins.
f)
public int getHeight() { if(left == null && right == null) return 1; if(left == null) return 1 + right.getHeight(); if(right == null) return 1 + left.getHeight(); return 1 + Math.max(left.getHeight(), right.getHeight()); }
g)
void getInOrderHelper(ArrayList<Integer> a){ if(left != null) left.getInOrderHelper(a); a.add(data); if(right != null) right.getInOrderHelper(a); }
h)
2. und 3. Antwort sind richtig
Aufgabe 3 - Streutabellen
a)
boolean exists(int h) { if(h >= urls.size() || urls.get(h).isEmpty()) return false; return true; }
b)
Mit der Kollisionsliste ist die ArrayList eines Buckets gemeint, durch die Kollisionen aufgelöst werden.
int getIndex(String url, ArrayList<String> urlList) { for(int i = 0; i < urlList.size(); i++) { if(urlList.get(i).equals(url)) return i; } return -1; }
Alternativ:
int getIndex(String url, ArrayList<String> urlList) { return urlList.indexOf(url); }
Bemerkung:
Der Parameter urlList ist eigentlich überflüssig, da man mit Hilfe der url und der Hashfunktion die korrekt urlList selbstständig identifizieren kann.
c)
String loopkup(String url) throws UnknownHostException { int h = hash(url); if(!exists(h)) throw new UnknownHostException(); ArrayList<String> bucket = urls.get(h); int index = getIndex(url, bucket); if(index == -1) throw new UnknownHostException(); return ips.get(h).get(index); }
d)
void resize(int h) { while(urls.size() <= h) { urls.add(new ArrayList<String>()); ips.add(new ArrayList<String>()); } }
alternativ:
void resize(int h) { urls.ensureCapacity(h); ips.ensureCapacity(h); }
e)
void register(String url, String ip){ int h = hash(url); // Hashtabelle vergrößern (resize verändert nichts, wenn ein Vergrößern nicht notwendig ist) resize(h); int index = getIndex(url, urls.get(h)); // URL wurde nicht gefunden -> URL und IP neu hinzufügen if(index == -1) { urls.get(h).add(url); ips.get(h).add(ip); // URL ist bereits vorhanden -> aktualisiere IP } else { ips.get(h).set(index, ip); } }
Bemerkung:
Die Aufgabe baut auf der Annahme auf, dass es sich praktisch um zwei eigenständige, aber gleichzeitig (!) verwaltete Hashtabellen handelt.
Nur aufgrund diese Annahme funktionieren die obigen Funktionen korrekt.
Aufgabe 4 - Dynamische Programmierung
a)
public static boolean isPrimeDP(long p, long primes[]) { for(int i = 0; primes[i] * primes[i] <= p; i++) { if(primes[i] != 0 && p % primes[i] == 0) return false; } return true; }
Optimierung beim Abbruchskriterium des naiven Primzahltests:
Überprüfe nur alle Primzahlen zwischen 2 und √n
b)
public static long getPrimeDPHelper(int n, long primes[]) throws ArrayIndexOutOfBoundsException { // ArrayIndexOutOfBoundsException detection (falls getPrimeDPHelper(..) falsch aufgerufen wird) if (n >= primes.length) { throw new ArrayIndexOutOfBoundsException("Uebergebenes Array zum Speichern der berechneten Primzahlen ist zu klein!"); } if (n <= 0) return 2; // Geforderte Primzahl wurde noch nicht berechnet if (primes[n] == 0) { // Berechne den vorherige Primzahl long p = getPrimeDPHelper(n - 1, primes); // Berechne ausgehend von der vorherigen, die aktuelle Primzahl do { p++; } while(!isPrimeDP(p, primes)); primes[n] = p; } return primes[n]; }
Programm zum selber Testen: :pruefungen:bachelor:aud:primes.java.txt
Aufgabe 5 - Graphen
a)
| Kara | A | B | C | D | E | Klee |
|---|---|---|---|---|---|---|
| [0] | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| 0 | ∞ | 18 | [3] | 7 | 9 | ∞ |
| 0 | 13 | 18 | 3 | [7] | 7 | ∞ |
| 0 | 13 | 18 | 3 | 7 | [7] | 19 |
| 0 | [11] | 18 | 3 | 7 | 7 | 19 |
| 0 | 11 | [16] | 3 | 7 | 7 | 17 |
| 0 | 11 | 16 | 3 | 7 | 7 | [17] |
| 0 | 11 | 16 | 3 | 7 | 7 | 17 |
alternativ:
| Kara | A | B | C | D | E | Klee |
|---|---|---|---|---|---|---|
| [0] | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| ∞ | 18Klara | [3Klara] | 7Klara | 9Klara | ∞ | |
| 13C | 18Klara | 7Klara | [7C] | ∞ | ||
| 11E | 18Klara | [7Klara] | ∞ | |||
| [11E] | 18Klara | 19D | ||||
| [16A] | 17A | |||||
| [17A] | ||||||
Indizes rückwärts (von unten nach oben) durchgehen : [17A] → [11E] → [7C] → [3Klara] → [0]
⇒ umdrehen: Klara → C → E → A → Klee
b)
Kürzester Pfad:
Kara → C → E → A → Klee
c)
(Kara, C), (C, E), (E, A), (A, B), (A, Klee), (Kara, D)
Länge der Leitung: 29 (die Leitung in den zwei Kästchen unter A ist doppelt verlegt)
Aufgabe 6 - Formale Verifikation
a)
Induktionsanfang:
IA_0 (n = 0): C_0 = (0 + 2) * 2^(0 - 1) = 2 * 2^(-1) = 2 / 2 = 1 cpRec(0) = 1 (Basisfall) IA_1 (n = 1): C_1 = (1 + 2) * 2^(1 - 1) = 3*2^0 = 3 * 1 = 3 cpRec(1) = 3 (Basisfall)
Induktionsschritt:
Induktionsvorraussetzung:
IV_(n-2) (n-2): cpRec(n-2) = C_(n-2) gilt für ein n ∈ N_0 IV_(n-1) (n-1): cpRec(n-1) = C_(n-1) gilt für ein n ∈ N_0
Aus dem Programmfragment ist zu entnehmen:
cpRec(n) = 4 * cpRec(n-1) - 4 * cpRec(n-2) = ...
Über die obigen Induktionsvoraussetzungen kommt man auf:
... = 4 * C_(n-1) - 4 * C_(n-2) = = 4 * [((n - 1) + 2) * 2^((n - 1) - 1)] - 4 * [((n - 2) + 2) * 2^((n - 2) - 1)] = = 4 * [(n + 1) * 2^(n - 2)] - 4 * [n * 2^(n - 3)] = = 4 * (n + 1) * 2^(n - 2) - 4 * n * 2^(n - 3) = = 2^2 * (n + 1) * 2^(n - 2) - 2^2 * n * 2^(n - 3) = = (n + 1) * 2^2 * 2^(n - 2) - n * 2^2 * 2^(n - 3) = = (n + 1) * 2^(n - 2 + 2) - n * 2^(n - 3 + 2) = = (n + 1) * 2^n - n * 2^(n - 1) = = (n + 1) * 2^(n - 1) * 2 - n * 2^(n - 1) = = (2n + 2) * 2^(n - 1) - n * 2^(n - 1) = = 2^(n - 1) * (2n + 2 - n) = = 2^(n - 1) * (n + 2) = C_n
q.e.d.
b)
LO: Falsch n ≥ 0; a = 1; k = n - 1; p = 1; n > 0 (IF-Bedingung) (a = (n + 2) * 2^(n - 1)) = (1 = (n + 2) * 2^(n - 1)) -> kann nicht für jedes n ≥ 0 gelten RO: Falsch n ≥ 0; a = 1; k = n - 1; p = 1; n > 0 (IF-Bedingung) (p = 2^(n - k)) = (1 = 2^(n - (n - 1))) = (1 = 2^1) = (1 = 2) -> stimmt nicht LU: Richtig n ≥ 0; a = 1; k = n - 1; p = 1; n > 0 (IF-Bedingung) (p = 2^(n - k - 1) ∧ k ≥ 0) = (1 = 2^(n - (n - 1) - 1) ∧ n - 1 ≥ 0) = (1 = 2^0 ∧ n - 1 ≥ 0) = (1 = 1 ∧ n - 1 ≥ 0) Falls n eine Ganzzahl ist, folgt: (n > 0) ∧ (n - 1 ≥ 0) = true -> stimmt RU: Falsch n ≥ 0; a = 1; k = n - 1; p = 1; n > 0 (IF-Bedingung) (C_k = (k + 2) * p) = (C_(n-1) = (n + 1) * 1) = (C_(n-1) = n + 1) -> kann nicht für jedes n ≥ 0 gelten
c)
wp(A, I) =
wp("a = 1; k = n - 1; p = 1; if(n > 0)", p = 2^(n - k - 1) ∧ k ≥ 0) =
[(n > 0) ∧ wp("a = 1; k = n - 1; p = 1;", p = 2^(n - k - 1) ∧ k ≥ 0)] ∨ [n ≤ 0] =
[(n > 0) ∧ (1 = 2^(n - (n - 1) - 1) ∧ (n - 1) ≥ 0)] ∨ (n ≤ 0) =
[(n > 0) ∧ (1 = 2^0 ∧ n ≥ 1)] ∨ (n ≤ 0) =
(n ≥ 1) = (n > 0), da n Ganzzahl vom Typ long
[(n > 0) ∧ (1 = 1) ∧ (n > 0)] ∨ (n ≤ 0) =
[(n > 0) ∧ (true)] ∨ (n ≤ 0) =
(n > 0) ∨ (n ≤ 0) =
(true)
d)
Zu zeigen: {I ∧ b} => wp(A, I)
wp(A, I) =
wp("p = p * 2; k = k - 1;", p = 2^(n - k - 1) ∧ k ≥ 0) =
(p * 2 = 2^(n - (k - 1) - 1) ∧ (k - 1) ≥ 0) =
(p * 2 = 2^(n - k) ∧ k - 1 ≥ 0) =
(p * 2 = 2^(n - k) ∧ k ≥ 1) =
(k ≥ 1) = (k > 0), da k Ganzzahl vom Typ long
(p * 2 = 2^(n - k) ∧ k > 0)
{I ∧ b} => wp(A, I) =
{(p = 2^(n - k - 1) ∧ k ≥ 0) ∧ (k > 0)} => wp(A, I) =
¬{(p = 2^(n - k - 1) ∧ k ≥ 0) ∧ (k > 0)} ∨ wp(A, I) =
¬(p = 2^(n - k - 1)) ∨ ¬(k ≥ 0) ∨ ¬(k > 0) ∨ wp(A, I) =
(p ≠ 2^(n - k - 1)) ∨ (k < 0) ∨ (k ≤ 0) ∨ wp(A, I) =
(p ≠ 2^(n - k - 1)) ∨ (k ≤ 0) ∨ wp(A, I) =
(p ≠ 2^(n - k - 1)) ∨ (k ≤ 0) ∨ (p * 2 = 2^(n - k) ∧ k > 0) =
Überlegung:
(p * 2 = 2^(n - k)) =
(p = 2^(n - k) / 2) =
(p = 2^(n - k - 1))
Somit folgt:
(p ≠ 2^(n - k - 1)) ∨ (k ≤ 0) ∨ (p = 2^(n - k - 1) ∧ k > 1)
Und hieraus folgt offensichtlich:
Sind (p ≠ 2^(n - k - 1)) und (k ≤ 0) beide nicht erfüllt, dann muss (p = 2^(n - k - 1) ∧ k > 1) erfüllt sein.
Die Invariante ist somit gültig.
einfacher:
Zu zeigen: (I ∧ b) => wp(B, I)
I: p = 2^(n - k - 1) ∧ k ≥ 0
b: (k > 0)
B: "p *= 2; k--" <=> "p = p * 2; k = k - 1;"
(I ∧ b):
p = 2^(n - k - 1) ∧ k ≥ 0 ∧ k > 0
<=> p = 2^(n - k - 1) ∧ k > 0 (weil: (k ≥ 0 ∧ k > 0) <=> (k > 0))
wp(B, I):
wp("p = p * 2; k = k - 1;", p = 2^(n - k - 1) ∧ k ≥ 0)
<=> wp("p = p * 2;", p = 2^(n - (k - 1) - 1) ∧ k - 1 ≥ 0)
<=> wp("p = p * 2;", p = 2^(n - k) ∧ k ≥ 1)
<=> wp(" ", p * 2 = 2^(n - k) ∧ k ≥ 1)
<=> p * 2 = 2^(n - k) ∧ k ≥ 1
<=> p = (1/2) * 2^(n - k) ∧ k ≥ 1
<=> p = 2^(n - k) * (1/2) ∧ k ≥ 1
<=> p = 2^(n - k) * 2^(-1) ∧ k ≥ 1 (weil: (1/2) = 2^(-1))
<=> p = 2^(n - k - 1) ∧ k ≥ 1 (weil: 2^(n - k) * 2^(-1) = 2^(n - k - 1))
(I ∧ b) => wp(B, I):
p = (2^(n - k - 1) ∧ k > 0) => (p = 2^(n - k - 1) ∧ k ≥ 1)
-> wahr, weil k > 0 <=> k ≥ 1, da k vom Datentyp "long" und damit ganzzahlig (..., -2, -1, 0, 1, 2, ...)
fertig
e)
V := k
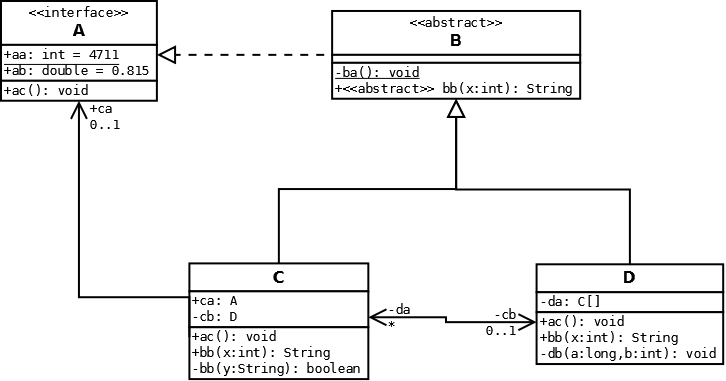
Aufgabe 7 - UML
Dia Sourcefile (für etwaige Korrekturen): :pruefungen:bachelor:aud:08-2011-uml.dia.txt