Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 - Wissensfragen
a) [Nicht mehr Stoff aktueller Semester]
b) (unsicher)
- O(log n)
- O(n²)
- O(2^n)
c) Falsch, der Balancefaktor entspricht der Differenz der beiden Höhen
d) Falsch, implizit (also automatisch) geht es nur in die andere Richtung (Ober o = new Unter();). Explizit mit Cast geht zur Compilezeit (Unter u = (Unter) new Ober();) auch, wirft aber eine ClassCastException zur Laufzeit.
e) Richtig
f) Richtig, beispielsweise oft beim Comparable Interface benutzt: LinkedList<Comparable>
g) Falsch, HeapSort ist in-place
h) O(n²)
i) richtig, O(|v| + |E|)
Aufgabe 2 - UML
a)
Anmerkung:
Bei dem gegebenen UML-Klassendiagramm wird keine grafische Unterscheidung zwischen „implements“ und „extends“ getroffen.
In Java gilt jedoch:
Interface extends Interface // OK Interface implements Interface // Falsch Interface extends Class // Falsch Interface implements Class // Falsch Class extends Interface // Falsch Class implements Interface // OK Class extends Class // OK Class implements Class // Falsch // Wobei jede Class auch abstract sein kann
Daher sind die Pfeile immer eindeutig.
abstract class EierLegend implements Haustier { protected int eierSammeln() { // ... } } class Schaf extends WolleGebend implements Schlachtvieh, MilchErzeugend { public static final int SCHWARZ = 1; private static int anzahl = 0; public float melken() { // ... } public final void schlachten() { // ... } protected static int zaehlen() { // ... } }
b)
In Java ist (im Gegensatz zu manchen anderen Programmiersprachen) keine Mehrfachvererbung möglich. Die Klasse EierlegendeWollMilchSau erbt jedoch von den Klassen EierLegend, WolleGebend und Sau.
c)
Die Klassen EierLegend und WolleGebend sollten als Interface implementiert werden, ebenso, wie MilchErzeugend und SchlachVieh bereits Interfaces sind.
„Eigenschaften“ bzw. „Schnittstellen“ sollte ohnehin eher als Interface, als abstrakte Klasse implementiert werden.
Liste aller Änderungen:
- interface EierLegend
- interface WolleGebend
- Huhn implements EierLegend
- Schaf implements WolleGebend
- EierLegend extends Haustier
- WolleGebend extends Haustier
- EierlegendeWollMilchSau implements EierLegend
- EierlegendeWollMilchSau implements WolleGebend
d)
UML-Sequenzdiagramm
Aufgabe 3 - Rekursion
a)
Kaskadenartige, verschränkte Rekursion
b)
public static int foo(int n) { int ret; if (n == 0) { ret = 3; } else if (n == 1) { ret = 1; } else { ret = foo(n - 1) + bar (n - 2); } return ret; }
c)
bar(3)
---> foo(3)
--->foo(2)
--->foo(1)
--->bar(0)
--->bar(1)
---> bar(2)
--->foo(2)
--->foo(1)
--->bar(0)
--->bar(1)
d)
Es werden immer wieder die selben Wert neu berechnet z. b. foo(2). Optimierung durch dynamische Programmierung
e)
public static int foo(int n) { int ret; if(fooTable[n] == UNKNOWN) { // <Teilabschnitt von a)> if (n == 0) { ret = 3; } else if (n == 1) { ret = 1; } else { ret = foo(n - 1) + bar (n - 2); } // </Teilabschnitt von a)> fooTable[n] = ret; } ret = fooTable[n]; return ret; }
e)
- Laufzeit: O(n), da man, um von bar(n) auf bar(n + 1) zu kommen, lediglich die Aufrufe foo(n) und bar(n) zu berechnen sind und alle anderen Ergebnisse bereits in der Tabelle stehen
- Speicherbedarf: O(n), da man zwei Arrays der Größe (n + 1) beneq05oqabötigt (je eins für DP von foo und von bar)
Aufgabe 4 - Sortieren
a)
Die Zahlen werden von hinten (rechts) nach vorne (links) sortiert, damit bspw. die Zahl „78“ vor der Zahl „88“ steht. Wichtig ist hierbei, dass das Verfahren unbedingt stabil sortieren muss.
b)
| Stelle | Reihung | |||||
|---|---|---|---|---|---|---|
| 420 | 234 | 142 | 123 | 432 | 230 | |
| 3 | 420 | 230 | 142 | 432 | 123 | 234 |
| 2 | 420 | 123 | 230 | 432 | 234 | 142 |
| 1 | 123 | 142 | 230 | 234 | 420 | 432 |
c)
Anmerkung:
Mit Angabe von „from“ und „to“ wird eine Teilsortierung moeglich.
Beispiel-Code zur Aufgabe: https://fsi.cs.fau.de/forum/post/160481;nocount
public static void sortPos(int array[], int from, int to, int pos) { LinkedList<Integer>[] buckets = new LinkedList[10]; //Für jede Ziifer 0-9 einen Bucket erstellen for (int i = 0; i < buckets.length; i++) { //In jedem Bucket eine LinkedList erstellen buckets[i] = new LinkedList(); } for (int i = from; i < to; i++) { //Buckets mit PLZs befüllen und sortieren int b = getDigit(array[i], pos); buckets[b].addLast(array[i]); } LinkedList<Integer> master = new LinkedList<>(); //Master Liste erstellen in die Werte sortiert kopiert werden können for (int i = 0; i < buckets.length; i++) { //In Master Liste einen Bucket nach dem anderen kopieren master.addAll(buckets[i]); } for(int i = from; i < to; i++) { //In ursprünglichen Array die Elemente aus Master Liste kopieren. array[i] = master.removeFirst(); } } public static void radixSort(int[] array) { for (int i = 5; i >=1; i--) { sortPos(array, 0, array.length, i); } }
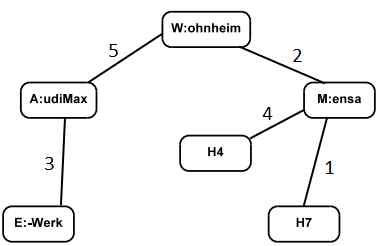
Aufgabe 5 - Graphen
a)
| A | E | H4 | H7 | M | W | Warteschlange |
|---|---|---|---|---|---|---|
| ∞ | ∞ | ∞ | ∞ | ∞ | [0] | W |
| 15 | ∞ | ∞ | ∞ | [2] | 0 | A, M |
| 15 | ∞ | 6 | [3] | 2 | 0 | A, H4, H7 |
| 15 | 21 | [6] | 3 | 2 | 0 | A, H4, E |
| [14] | 20 | 6 | 3 | 2 | 0 | A, E |
| 14 | [18] | 6 | 3 | 2 | 0 | E |
| 14 | 18 | 6 | 3 | 2 | 0 |
b)
c)
- Eulerpfad: Nein, da man mindestens eine Kante mehrmals benutzen müsste. Es weisen mehr als 2 Knoten einen ungeraden Grad auf.
- Eulerzyklus: Nein, es haben nicht alle Knoten einen geraden Grad.
d)
Anmerkung:
Je nach Implementierung sind hier viele Möglichkeiten denkbar.
Dijkstra: O(v log(v) + e) bei einer Implementierung mit Fibonacci-Heap
Kruskal: O(e * log(e)) bei Implementierung mit Pfadkompression
Aufgabe 6 - Streutabellen
a)
| Bucket | Keys (LinkedList) |
|---|---|
| 0 | |
| 1 | 27 → 75 |
| 2 | |
| 3 | 44 → 4 → 0 |
| 4 | |
| 5 | 13 → 65 → 33 |
| 6 | |
| 7 | 46 → 26 |
b)
Die Hashfunktion mappt jeden Schlüssel garantiert auf einen Bucket mit ungerader Nummer.
Begründung:
Die Multiplikation mit 2 macht aus jedem Schlüssel garantiert eine gerade Zahl, die anschließende Addition mit 3 garantiert eine ungerade Zahl.
Eine ungerade Zahl modulo eine gerade Zahl ergibt wiederum eine ungerade Zahl.
c)
Primärkollision, wenn Bucket, wo es eigentlich eingefügt werden sollte, ein D hat. Sekundärkollision, wenn Bucket, wo es eigentlich eingefügt werden sollte, ein P oder S hat.
| Bucket | Key | P, S oder D |
|---|---|---|
| 0 | 12 | S |
| 1 | 33 | D |
| 2 | 66 | S |
| 3 | 28 | P |
| 4 | 14 | D |
| 5 | 6 | S |
| 6 | 18 | D |
| 7 | 5 | D |
| 8 | 15 | P |
| 9 | 9 | D |
Aufgabe 7 - wp-Kalkül
a)
wp("a += ++b - 2;", a + b > 0) =
wp("b = b + 1; a = a + b - 2;", a + b > 0) =
wp("b = b + 1;", (a + b - 2) + b > 0) =
((a + (b + 1) - 2) + (b + 1) > 0) =
(a + b - 1 + b + 1 > 0) =
(a + 2 * b > 0)
b)
wp("if (a > -2*b && b > 0) {a += ++b - 2;} else {b -= --a;}", a + b > 0) =
[(a > -2*b ∧ b > 0) ∧ wp("a += ++b - 2;", a + b > 0)] ∨ [(¬(a > -2*b ∧ b > 0) ∧ wp("b -= --a;", a + b > 0)] =
bereits in der a) berechnet:
wp("a += ++b - 2;", a + b > 0) = (a + 2 * b > 0)
durch die Aufgabenstellung gegeben:
wp("b -= --a;", a + b > 0) = (b > 0)
damit ergibt sich:
= [(a > -2*b ∧ b > 0) ∧ (a + 2*b > 0)] ∨ [(¬(a > -2*b ∧ b > 0) ∧ (b > 0)] =
[(a > -2*b) ∧ (b > 0) ∧ (a + 2*b > 0)] ∨ [((a ≤ -2*b) ∨ (b ≤ 0)) ∧ (b > 0)] =
[(a > -2*b) ∧ (b > 0) ∧ (a + 2*b > 0)] ∨ [(a ≤ -2*b) ∧ (b > 0)] =
[(a > -2*b) ∧ (b > 0) ∧ (a > -2*b)] ∨ [(a ≤ -2*b) ∧ (b > 0)] =
[(a > -2*b) ∧ (b > 0)] ∨ [(a ≤ -2*b) ∧ (b > 0)] =
(b > 0)
c)
i)
Antwort 1: Falsch c = 1, d = 1, e = 1, a ≥ b ≥ 0 (a b) = c / d c / d = 1 / 1 = 1 Kann offensichtlich nicht für jedes a und b gelten Antwort 2: Falsch c = 1, d = 1, e = 1, a ≥ b ≥ 0 c = (a + 1 - b)! - e! ∨ d = (e + 1)! (d = (e + 1)!) = (1 = (1 + 1)! = 2) kann nicht stimmen (c = (a + 1 - b)! - e!) = (1 = (a + 1 - b)! - 1!) = (0 = (a + 1 - b)!) kann offensichtlich nicht für jedes a und b gelten Antwort 3: Richtig c = 1, d = 1, e = 1, a ≥ b ≥ 0 c = a! / (a - e + 1)! ∧ d = (e - 1)! (d = (e - 1)!) = (1 = (1 - 1)!) = (1 = 0!) = (1 = 1) = (true) (c = a! / (a - e + 1)!) = (1 = a! / (a - 1 + 1)!) = (1 = a! / a!) = (1 = 1 / 1) = (true) gültig! Antwort 4: Falsch c = 1, d = 1, e = 1, a ≥ b ≥ 0 1 ≤ c ≤ a! - b! (1 ≤ c ≤ a! - b!) = (1 ≤ 1 ≤ a! - b!) Kann offensichtlich nicht für jedes a und b gelten
ii)
Invariante nachweisen:
Zu zeigen: {I ∧ b} => wp(A, I)
wp(A, I) =
wp("c = c * (a + 1 - e); d = d * e; e = e + 1;", c = a! / (a - e + 1)! ∧ d = (e - 1)!) =
wp("c = c * (a + 1 - e); d = d * e;", c = a! / (a - (e + 1) + 1)! ∧ d = ((e + 1) - 1)!) =
wp("c = c * (a + 1 - e);", c = a! / (a - (e + 1) + 1)! ∧ d * e = ((e + 1) - 1)!) =
(c * (a + 1 - e) = a! / (a - (e + 1) + 1)! ∧ d * e = ((e + 1) - 1)!) =
(c * (a + 1 - e) = a! / (a - e)! ∧ d * e = e!)
{I ∧ b} => wp(A, I) =
{(c = a! / (a - e + 1)! ∧ d = (e - 1)!) ∧ (e ≤ b)} => wp(A, I) =
¬{(c = a! / (a - e + 1)!) ∧ (d = (e - 1)!) ∧ (e ≤ b)} ∨ wp(A, I) =
(c ≠ a! / (a - e + 1)!) ∨ (d ≠ (e - 1)!) ∨ (e > b) ∨ wp(A, I) =
(c ≠ a! / (a - e + 1)!) ∨ (d ≠ (e - 1)!) ∨ (e > b) ∨ (c * (a + 1 - e) = a! / (a - e)! ∧ d * e = e!) =
Überlegung:
Gelten (c ≠ a! / (a - e + 1)!) und (d ≠ (e - 1)!) beide nicht, dann gilt offensichtlich:
(c = a! / (a - e + 1)!) ∨ (d = (e - 1)!)
Für diesen Fall müssen wir zeigen, dass dann (c * (a + 1 - e) = a! / (a - e)! ∧ d * e = e!) gilt
(d * e = e!) = (d = e! / e) = (d = (e - 1)!)
-> gilt
(c = a! / (a - e + 1)!) gilt, das heißt wir können das in (c * (a + 1 - e) = a! / (a - e)!) einsetzen:
((a! / (a - e + 1)!) * (a + 1 - e) = a! / (a - e)!) =
(a! / (a - e + 1 - 1)! = a! / (a - e)!) =
(a! / (a - e)! = a! / (a - e)!) =
(true)
-> gilt ebenfalls
Damit ist die Invariante gültig.