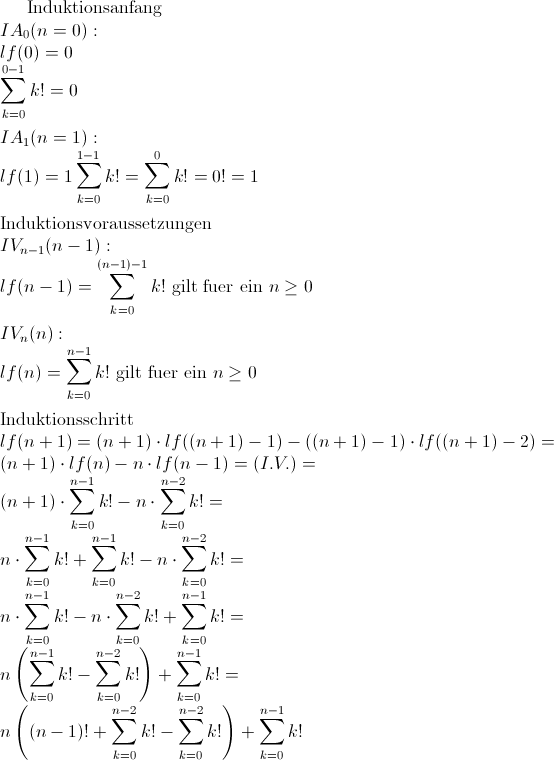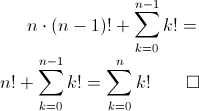Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen (Übersicht)
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 - Wissensfragen
a) 2. Antwort ist richtig: Θ(x²)
Hierfür multipliziert man den Term aus, und macht dann eine Grenzwertbetrachtung Limes x → ∞
Tipp: Höchste Potenz im Zähler- und Nenner ausklammern und kürzen. Terme der Form c/x gehen bei x → ∞ selbst gegen 0.
b) 2. Antwort ist richtig: O(n * (log n)²)
Die Schleife selbst wird O(log n) mal ausgeführt. Pro Schleifendurchlauf wird Folgendes berechnet:
a = goo(n) in O(n), b = goo(n) in O(n), c = bar(n) in O(n log n) und d = zoo(a, b, c) in O(1)
Somit ist der Gesamtaufwand eines Schleifendurchlaufs: O(n) + O(n) + O(n log n) + O(1) = O(n log n)
Da es O(log n) Schleifendurchläufe gibt, ist der Gesamtaufwand von foo(n): O(log n) * O(n log n) = O(n (log n)²)
c) Falsch
Im Allgemeinen sollten sie teilerfremd sein, bzw. der ggT so klein (am Besten 1) wie möglich.
Man stelle sich z.B. n = 10, m = 20 vor. Der ggT lautet 10 und jeglicher Wert k wird immer auf 0 oder 10 gehasht.
d)
Einfach verkettete Liste: Θ(n)
Obwohl das Element e, das gelöscht werden soll, zur Verfügung steht, ist der der Vorgänger unbekannt. Die Liste muss trotzdem von Vorne durchgegangen werden.
Doppelt verkettete Liste: Θ(1)
Das zu löschende Element hat Zeiger auf Vorgänger und Nachfolger. Damit lässt sich das Löschen mit zwei Zeigermanipulationen tätigen: e.prev.next = e.next, e.next.prev = e.prev
e) 4. Antwort ist richtig: [15, 8, 23]
f) Richtig, Mergesort kann als externes Sortierverfahren verwendet werden.
g) 3. Antwort ist richtig: ceil(log_k(n)) + 1
h) Falsch, in einem stark zusammenhängenden Graphen existiert von jedem Knoten zu jedem anderen Knoten ein Pfade, nicht zwangsläufig jedoch eine Kante.
i) Richtig, egal wie viele Nachfolger der Knoten hat, die gesamte Zeile (Länge n) der Matrix für diesen Knoten muss durchgegangen werden.
j) 2. und 3. Antwort ist richtig.
Postorder bedeutet: „Links, Rechts, Mitte“.
k) 2. Antwort ist richtig: Θ(n³)
Der Aufwand für Floyd beträgt Θ(n³). Den kürzesten Pfad zwischen zwei Knoten kann man in Θ(m) finden, wobei m die Länge dieses Pfades ist.
Nachdem ein Pfad von v nach u höchstens die Länge n haben kann, Pfade in die Rückrichtung von u nach v nicht zwangsläufig die gleiche Länge haben müssen und es n Knoten gibt,
lautet die worst-case Abschätzung: O(n²)
Insgesamt gilt jedoch: Θ(n³) + O(n²) = Θ(n³)
l) 2. Antwort ist richtig: Θ(n + m)
Für den Spezialfall, dass alle Kanten das gleiche Gewicht haben, zählt praktisch nur die Pfadlänge, also die Anzahl an Kanten, die man bis zum Zielknoten ablaufen musste.
Dies lässt sich somit mit einer Breitensuche im Graphen realisieren, da hier zunächst die Knoten besucht werden, die „1 Kante“ von v entfernt sind, danach die, die „2 Kanten“ entfernt sind, etc.
Der Aufwand einer Breitensuche beträgt Θ(n + m)
m) 3. Antwort ist richtig: mindestens 1
Aufgabe 2 - Dynamische Programmierung
BigInteger[] dpArr = new BigInteger[Short.MAX_VALUE]; BigInteger dp(int n) { if(n <= 0 || n >= Short.MAX_VALUE) { return ZERO; } else if(n == 1) { return ONE; } else { if(dpArr[n] == null) dpArr[n] = sub(mul(n, dp(n - 1)), mul(n - 1, dp(n - 2))); return dpArr[n]; } }
Sourcefile zum selber Testen: :pruefungen:bachelor:aud:leftfactorial.java.txt
Aufgabe 3 - Schreibtischlauf
## fld[0][0] ## ## fld[0][1] ## ## fld[0][2] ## 0,0 0,1 0,2 NPE null null Grmbl ## fld[1][0] ## ## fld[1][1] ## ## fld[1][2] ## 1,0 1,1 1,2 x x x icks Mitte ## fld[2][0] ## ## fld[2][1] ## ## fld[2][2] ## 2,0 2,1 2,2 null Fertig
Sourcefile zum selber Testen: :pruefungen:bachelor:aud:omega.java.txt
Aufgabe 4 - Induktionsbeweis
Aufgabe 5 - Rekursion
Gesamter Sourcecode zum selber Testen: :pruefungen:bachelor:aud:riddle.java.txt
a)
boolean isSolution(LinkedList<Node> p) { int tmpRes = p.get(0).val; for(int i = 1; i < p.size() - 1; i+= 2) { Node op = p.get(i); Node v = p.get(i+1); switch(op.type) { case ADD: tmpRes += v.val; break; case SUB: tmpRes -= v.val; break; case MUL: tmpRes *= v.val; break; case DIV: if(tmpRes % v.val != 0) return false; tmpRes /= v.val; break; case EQ: if(v.result && tmpRes == v.val) return true; return false; default: return false; } } return false; }
b)
void allPaths(Node n, LinkedList<Node> p, LinkedList<LinkedList<Node>> s) { if(n.visited) return; n.visited = true; if(n.result) { p.addLast(n); addList(p, s); p.removeLast(); n.visited = false; } else { p.addLast(n); for(Node neighbour : n.neighbours) allPaths(neighbour, p, s); p.removeLast(); n.visited = false; } }
c)
LinkedList<Node> solve(Node start) { LinkedList<LinkedList<Node>> s = new LinkedList<>(); allPaths(start, new LinkedList<Node>(), s); LinkedList<Node> best = null; for(LinkedList<Node> path : s) { if(isSolution(path)) { if(best == null || path.size() < best.size()) best = path; } } return best; }
Aufgabe 6 - Abstrakte Datentypen
a)
ops: add: Nat x Nat -> Nat axs: add(zero, y) = y add(succ(x), y) = succ(add(x, y))
b)
ops: fib: Nat -> Nat axs: fib(zero) = succ(zero) fib(succ(zero)) = succ(zero) fib(succ(succ(n))) = add(fib(succ(n)), fib(n))
c)
ops: equals: Nat x Nat -> Nat axs: equals(zero, zero) = zero equals(zero, x) = succ(zero) equals(x, zero) = succ(zero) equals(succ(x), succ(y)) = equals(x, y)
d)
ops: mult: Nat x Nat -> Nat axs: mult(zero, zero) = zero mult(succ(x), y) = add(mult(x,y), y)
Aufgabe 7 - Sortieren
Vollständiger Sourcecode zum selber Testen: :pruefungen:bachelor:aud:sort.java.txt
a)
void prepareGroups(int left, int right) { int lower = left; while(lower <= right) { int median = lower + 2; int upper = lower + 4; if(upper > right) { upper = right; median = lower + (upper - lower) / 2; } groupSort(lower, upper); swap(lower, median); lower += 5; } }
b)
void pivotFirst(int left, int right) { if(left >= right) return; prepareGroups(left, right); int nextMedianPos = left; for(int i = left; i <= right; i+= 5) swap(i, nextMedianPos++); pivotFirst(left, nextMedianPos - 1); }
c)
void quickSortMedian(int left, int right) { if(left < right) { int indexOfPivot = left; pivotFirst(left, right); int index = partition(left, right, left); quickSortMedian(left, index - 1); quickSortMedian(index + 1, right); } }
d)
Hierbei geht es nicht um obigen Algorithmus, sondern allgemein um einen Quicksort-Algorithmus, der vor jeder Partitionierung
den Median alle betrachteten Werte untersucht.
Mit Master-Theorem:
T = 2 * T(n/2) + n a = 2, b = 2, f(n) = n Fall 2: f(n) ∈ Θ(n^(log_b(a))) n ∈ Θ(n^(log_2(2))) n ∈ Θ(n^1) n ∈ Θ(n) true Damit gilt: T(n) ∈ Θ(n * log n)
Lösung: O(n * log n)
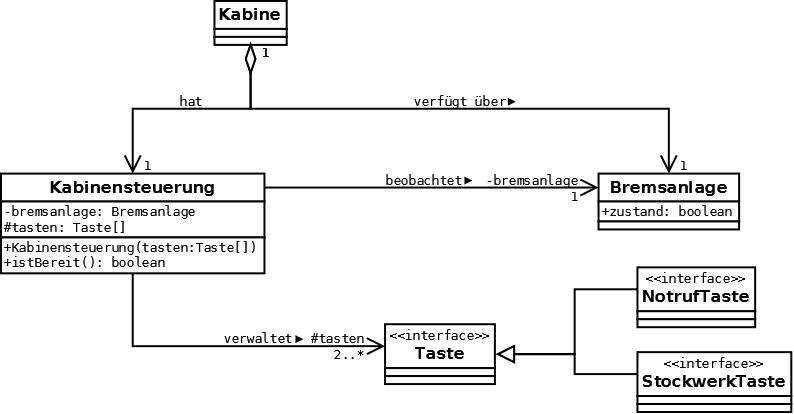
Aufgabe 8 - UML
Dia-Sourcefile für etwaige Korrekturen: :pruefungen:bachelor:aud:21-02-2013-8.dia.txt
Vorsicht, dieses Diagramm ist falsch. Erstens müssen bremsanlage und tasten nicht mit in Kabinensteuerung, sondern nur als Beziehung eingetragen werden. Außerdem sollte die implements Beziehung zwischen den Tasten und dem Interface gestrichelt sein.
Aufgabe 9 - Formale Verifikation
a)
LO: Falsch, r bleibt während der Abarbeitung der Schleife offensichtlich nicht konstant RO: Richtig LU: Falsch, ist vor der Schleife ungültig RU: Falsch, ist zwar vor der Schleife erfüllt, stimmt während der Abarbeitung der Schleife nicht
b)
Zu zeigen: P => wp(A, I)
wp(A, I) = wp("r = 1; t = e;", b^e = r * b^t) =
= (b^e = 1 * b^e) = (true)
(P => true) = (true)
c)
Zu zeigen: {I ∧ b} => wp(S, I)
wp(S, I) = wp("r = r * b; t = t - 1;", b^e = r * b^t) =
= (b^e = r * b * b^(t-1)) =
= (b^e = r * b^t) =
{I ∧ b} => wp(S, I) =
(b^e = r * b^t ∧ t != 0) => (b^e = r * b^t) =
true
d)
Zu zeigen: {I ∧ ¬b} => wp(S, Q) // S leer
{I ∧ ¬b} => Q =
(b^e = r * b^t ∧ t = 0) => (b^e = r) =
true
e)
V = t