Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen (Übersicht)
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 - Binärsuche
a) O(n)
b)
static int rateZahlSchnell(int n) { if(n < 0) return -1; int start = 0; int end = n; do { int mid = (start + end) / 2; int ret = testeLoesung(mid); if(ret == 0) return mid; if(ret > 0) start = mid + 1; if(ret < 0) end = mid - 1; } while(start <= end); return -1; } static int testeLoesung(int lsg) { int number = 42; if(lsg < number) { return 1; } else if(lsg > number) { return -1; } else { return 0; } }
c) O(log n)
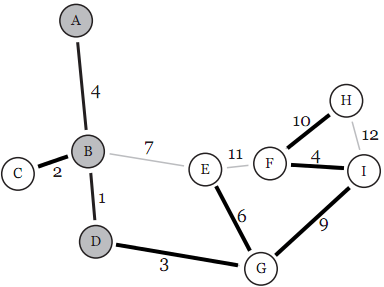
Aufgabe 2 - Graphen
a)
- Ja
- Ja, ein Wurzelgraph ist ein DAG mit nur einer Wurzel
- Nein, es ist Tiefensuche
- Nein, in O(n)
- Nein, sie ist iterativ
b)
- Nein, es gibt Zyklen und der Graph ist ungerichtet
- Nein, es gibt Knoten, die mit nur einer Kante mit dem restlichen Graphen verbunden sind (Beispiel: Knoten C)
- Nein, es gibt Zyklen
- Ja, jeder Knoten ist von jedem anderen aus erreichbar
- Nein, nicht jeder Knoten hat einen geraden Grad
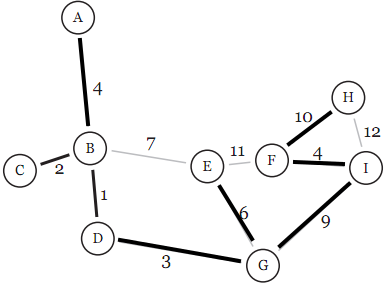
c)
| A | B | C | D | E | F | G | H | I |
|---|---|---|---|---|---|---|---|---|
| ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | [0] | ∞ |
| ∞ | ∞ | ∞ | ∞ | ∞ | [10] | ∞ | 0 | 12 |
| ∞ | ∞ | ∞ | ∞ | 21 | 10 | ∞ | 0 | [12] |
| ∞ | ∞ | ∞ | ∞ | [21] | 10 | 21 | 0 | 12 |
| ∞ | 28 | ∞ | ∞ | 21 | 10 | [21] | 0 | 12 |
| ∞ | 28 | ∞ | [24] | 21 | 10 | 21 | 0 | 12 |
| ∞ | [25] | ∞ | 24 | 21 | 10 | 21 | 0 | 12 |
| 29 | 25 | [27] | 24 | 21 | 10 | 21 | 0 | 12 |
d) 27
e)
AB, BD, BC, DG, GE, GI, IF, FH
f)
BD, BC, DG, BA, FI, GE, GI, FH
Aufgabe 3 - Java
a) Java Datei zum Ausprobieren: :pruefungen:bachelor:aud:test.java-ws07.txt
| Zeile | Fehler bzw. Ausgabe |
|---|---|
| 32 | 5 |
| 33 | 13 |
| 34 | 6 |
| 35 | 13 |
| 38 | 5 |
| 39 | 21 |
| 40 | 21 |
| 41 | 7 |
| 44 | FEHLER |
| 45 | 21 |
| 46 | FEHLER |
| 47 | 7 |
b)
| Zeile | Fehlerbeschreibung oder korrigierte Anweisung |
|---|---|
| 6 | fehlender Cast von double zu int |
| 8 | Vergleich („==“) statt Zuweisung („=“) |
| 12 | Variable „i“ hier nicht deklariert |
| 14 | Zuweisung („=“) statt Vergleich („==“) für booleschen Ausdruck |
| 15 | überzähliges „{“ am Ende der if-Bedingung |
c) Nein, eine Instanziierung von abstrakten Klassen ist nicht möglich.
Aufgabe 4 - Arithmetische Ausdrücke - Grammatik
(nicht mehr Stoff aktueller Semester)
Aufgabe 5 - ADT
a) Primärkonstruktoren:
- number
- binop
Sekundärkonstruktoren (war nicht gefragt):
- left
- right
- commutate
Projektionen:
- numops
b)
- numops(number(q)) = 0
- numops(binop(a,op,b)) = 1 + numops(a) + numops(b)
c)
- commutate(number(q)) = number(q)
- commutate(binop(a,*,b) = binop(communtate(b),*,commutate(a))
- commutate(binop(a,+,b) = binop(communtate(b),+,commutate(a))
- commutate(binop(a,-,b) = binop(communtate(a),-,commutate(b))
- commutate(binop(a,/,b) = binop(communtate(a),/,commutate(b))
d)
binop(left(commutate(binop(4,+,7))),*,right(binop(binop(1,-,1),+,binop(3,*,4)))) = //commutate// = binop(left(binop(7,+,4)),*,right(binop(binop(1,-,1),+,binop(3,*,4)))) = //right// = binop(left(binop(7,+,4)),*,binop(3,*,4)) = //left// = binop(7,*,binop(3,*,4))
e)
double left = left.evaluate(); double right = right.evaluate(); switch(op) { case '+': return left + right; case '-': return left - right; case '*': return left * right; case '/': return left / right; }
Aufgabe 6 - Rucksackproblem
a)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | [+] | / | / | / | / | / | / | / | / | / | / | / |
| 3 | - | [-] | / | + | + | / | / | / | / | / | / | / | / |
| 4 | - | - | / | - | - | [+] | / | + | + | / | / | / | / |
| 7 | - | - | / | - | - | - | / | - | - | / | + | + | [+] |
| 8 | - | - | / | - | - | - | / | - | - | + | - | - | [-] |
b)
Gesucht: Lösung für Rucksack der Größe 12
Elemente mit den Größen 1, 4, 7 (Pfad mit eckigen Klammern in der Tabelle aus a) markiert)
Algorithmus: P(5, 12) -> k_5 = 8 gehört nicht rein -> P(4, 12) P(4, 12) -> k_4 = 7 gehört rein -> P(3, 12 - 7) P(3, 5) -> k_3 = 4 gehört rein -> P(2, 5 - 4) P(2, 1) -> k_2 = 3 gehört nicht rein -> P(1, 1) P(1, 1) -> k_1 = 1 gehört rein -> Rucksack vollständig gefüllt
c)
for(int i = 1; i < n; i++) { // Zeilen for(int j = 0; j <= m; j++) { // Spalten // Fall P(n - 1, K): Gibt es in der Zelle direkt darüber eine Lösung, // dann ist P(n, K) = P(n - 1, K) // Das aktuelle Elemente gehört somit nicht zur Lösung -> OHNE if(tab[i - 1][j] != UNMOEGLICH) { tab[i][j] = OHNE; // Fall P(n - 1, K - k_n): Gibt es in der Zeile darüber, nach links versetzt // eine Lösung (Achtung: ArrayIndexOutOfBoundsException), dann ist // P(n, K) = P(n - 1, K) + k_n // Das aktuelle element gehört somit zur Lösung -> MIT } else if(elements[i] <= j && tab[i - 1][j - elements[i]] != UNMOEGLICH) { tab[i][j] = MIT; } } }
Vollständiges Programm:
:pruefungen:bachelor:aud:rucksack.java.txt
d)
- Ja
- Ja
- Ja, durch sukzessives Ausprobieren für Kapazitäten < m
- Nein, das Verfahren verwendet eine Integer-DP-Tabelle bzw. greift auf Indizes basierend auf der Elementgröße zu
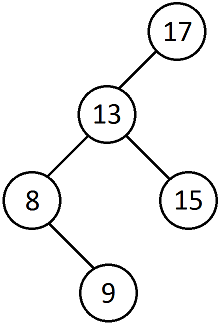
Aufgabe 7 - Binäre Bäume
a)
Der Binärbaum muss eine totale Ordnung aufweisen:
Alle Knoten im linken Teilbaum müssen einen echt kleineren, alle im rechten Teilbaum einen echt größeren Wert als der aktuelle Knoten haben.
b)
public class BB { ... public void einfuegen(int schluessel) { if(this.schluessel == schluessel) return; if(schluessel < this.schluessel) { if(left != null) { left.einfuegen(schluessel); } else { left = new BB(schluessel); } } else { if(right != null) { right.einfuegen(schluessel); } else { right = new BB(schluessel); } } } }
c)
public class BB { ... public int maximum() { if(right != null) return right.maximum(); return schluessel; } }
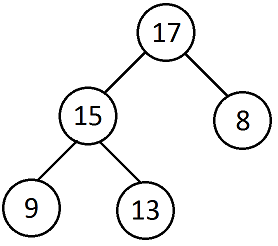
d) Der Wert eines Knotes in einem Max-Heap muss größer sein als der seiner Kinder.
e)
public class Heap { ... public int maximum() { return schluessel; } }
g)
- Nein
- Nein
- Ja, wenn es sich um einen Min-Heap handelt
- Nein, man muss eines Tiefensuche vewenden
Aufgabe 8 - Sortieren
a)
| ∨ | ||||||
| [35] | 70 | 42 | 11 | 99 | 1 | 20 |
| ∧ |
| ∨ | ||||||
| [35] | 70 | 42 | 11 | 99 | 1 | 20 |
| ∧ |
| ∨ | ||||||
| [35] | 20 | 42 | 11 | 99 | 1 | 70 |
| ∧ |
| ∨ | ||||||
| [35] | 20 | 42 | 11 | 99 | 1 | 70 |
| ∧ |
| ∨ | ||||||
| [35] | 20 | 42 | 11 | 99 | 1 | 70 |
| ∧ |
| ∨ | ||||||
| [35] | 20 | 1 | 11 | 99 | 42 | 70 |
| ∧ |
| ∨ | ||||||
| [35] | 20 | 1 | 11 | 99 | 42 | 70 |
| ∧ |
| ∨ | ||||||
| [35] | 20 | 1 | 11 | 99 | 42 | 70 |
| ∧ |
| ∨ | ||||||
| [35] | 20 | 1 | 11 | 99 | 42 | 70 |
| ∧ |
| ∨ | ||||||
| 11 | 20 | 1 | 35 | 99 | 42 | 70 |
| ∧ |
Linkes Teil-Array:
| ∨ | ||
| [11] | 20 | 1 |
| ∧ |
| ∨ | ||
| [11] | 20 | 1 |
| ∧ |
| ∨ | ||
| [11] | 1 | 20 |
| ∧ |
| ∨ | ||
| [11] | 1 | 20 |
| ∧ |
| ∨ | ||
| 1 | 11 | 20 |
| ∧ |
Linkes Teil-Array:
| ∨ |
| [1] |
| ∧ |
Rechtes Teil-Array:
| ∨ |
| [20] |
| ∧ |
Rechtes Teil-Array:
| ∨ | ||
| [99] | 42 | 70 |
| ∧ |
| ∨ | ||
| [99] | 42 | 70 |
| ∧ |
| ∨ | ||
| [99] | 42 | 70 |
| ∧ |
| ∨ | ||
| 70 | 42 | 99 |
| ∧ |
| ∨ | ||
| 70 | 42 | 99 |
| ∧ |
Linkes Teil-Array:
| ∨ | |
| [70] | 42 |
| ∧ |
| ∨ | |
| [70] | 42 |
| ∧ |
| ∨ | |
| 42 | 70 |
| ∧ |
Linkes Teil-Array:
| ∨ |
| [42] |
| ∧ |
Sortierte Folge:
| 1 | 11 | 20 | 35 | 42 | 70 | 99 |
b)
MyArray sort(MyArray a) { int len = a.getLength(); int halfLen = len / 2; if(len <= 1) return a; MyArray left = sort(getLeftSideSplit(halfLen)); MyArray right = sort(getRightSideSplit(halfLen)); return merge(left, right); }
c)
| / | mittlere Laufzeit | schlechteste Laufzeit | beste Laufzeit |
|---|---|---|---|
| QuickSort | O(n log n) | O(n²) | O(n log n) |
| MergeSort | O(n log n) | O(n log n) | O(n log n) |
| BubbleSort | O(n²) | O(n²) | O(n) |
Aufgabe 9 - Aufwände, O-Kalkül
a)
- O(log n)
- O(n), da k * n/2
- O(n²)
- O(n)
- O(n³)
b)
- Ja, Logarithmen zu verschiedenen Basen unterscheiden sich nur durch konstanten Faktor
- Ja, gültige Regel
- Nein, für Subtraktion und Division gibt es keine Sonderregeln
- Nein, O(n log n) steigt stärker
Aufgabe 10 - WP-Kalkül
a)
wp("b = 5*a - 3; c = 2*a; b = b + 3 * c;", b = 8) =
wp("b = 5*a - 3; c = 2*a;", b + 3*c = 8) =
wp("b = 5*a - 3;", b + 3*(2*a) = 8) =
((5*a - 3) + 3*(2*a) = 8) =
(5*a - 3 + 6*a = 8) =
(11*a = 11) =
(a = 1)
b)
wp("b = 2*a + 1; c = a*a; a = c + b*b;", a >= 0) =
wp("b = 2*a + 1; c = a*a;", c + b*b >= 0) =
wp("b = 2*a + 1;", a*a + b*b >= 0) =
(a*a + (2*a + 1)*(2*a + 1) >= 0) =
(a² + 4*a² + 4*a + 1 >= 0) =
(5* a² + 4*a + 1 >= 0) =
(true)
c)
wp("if (a == b) then a = 2*a; b = 2*b; else a = a + 1; b = b + 1; endif;", a = b) =
[(a == b) ∧ wp("a = 2*a; b = 2*b;", a = b)] ∨ [(a != b) ∧ wp("a = a + 1; b = b + 1;", a = b)] =
[(a == b) ∧ wp("a = 2*a;", a = 2*b)] ∨ [(a != b) ∧ wp("a = a + 1; b = b + 1;", a = b)] =
[(a == b) ∧ (2*a = 2*b)] ∨ [(a != b) ∧ wp("a = a + 1; b = b + 1;", a = b)] =
[(a == b) ∧ (2*a = 2*b)] ∨ [(a != b) ∧ wp("a = a + 1;", a = b + 1)] =
[(a == b) ∧ (2*a = 2*b)] ∨ [(a != b) ∧ (a + 1 = b + 1)] =
[(a == b) ∧ (a = b)] ∨ [(a != b) ∧ (a + 1 = b + 1)] =
(true) ∨ [(a != b) ∧ (a + 1 = b + 1)] =
(true) ∨ (false) =
(true)
d)
- Nein, gilt nur vor der Schleife, nicht im Schleifenrumpf
- Ja, gilt vor der Schleife nicht, jedoch: {I ∧ b} ⇒ wp(A, I)
- Nein, gilt nur vor der Schleife, nicht im Schleifenrumpf
- Ja, true ist immer Schleifeninvariante
e)
Invariante (y - y0) / (x - x0) = m Es gilt: x = x0; y = y0; x = x + 1; y = y + m; m unverändert ((y - y0) / (x - x0) = m) = ((y + m - y0) / (x + 1 - x0) = m) = ((y0 + m - y0) / (x0 + 1 - x0) = m) = (m / 1 = m) = (m = m) = (true)