Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Nebenfächer » mathematik » 1) Flüsse (Übersicht)
Inhaltsverzeichnis
LKOpt - Schriftliche Prüfung (10ECTS)
Dozent: Dieter Weninger
Erlaubte Hilfsmittel: Taschenrechner, Geodreieck, 4 Seiten handgeschriebener Hilfszettel
Zeit: 90 Minuten
Zeitlich ist die Klausur sehr knapp bemessen - lieber einmal mehr nochmal die abgeschriebenen Werte prüfen bevor man die Hälfte durchstreichen und nochmal rechnen muss (wie ich, der die falsche Basis im Simplex benutzt hat…)
Die Algorithmen und wichtigen Sätze passen gut auf zwei Seiten, besonders wenn man die Sortier- und Graphalgorithmen aus AuD noch gut kennt und nur die Unterschiede aufschreiben muss. Die dritte Seite habe ich genutzt, um die Lösungen einiger Übungsaufgaben aufzuschreiben - allerdings brauchte ich diese nicht. Besser wäre es gewesen, auch die Sätze, die auf den Übungsblättern bewiesen wurden, mitzunehmen. Es gibt keine „unwichtigen“ Sätze - jedes kleine Detail könnte helfen. Als Beispiel dient 4c): der benötigte Satz steht nicht im Skript, sondern wurde als Übungsaufgabe bewiesen.
Ich habe versucht, die Aufgabenstellungen so genau wie möglich wiederzugeben - ist natürlich kaum machbar, aber ich denke, dass die hier beschriebenen Probleme ähnlich genug zu denen aus der Prüfung sind.
Notiz am Rande: LKOpt bietet auch eine 5 ECTS-Prüfung an (entweder nur lineare oder nur kombinatorische Optimierung), die normalerweise ebenfalls schriftlich ist. Dieses Semester haben sich aber nur wenige Leute dafür angemeldet (6?), wodurch sie stattdessen als mündliche Prüfungen abgehalten wird. Falls jemand plant, diese Prüfung zu machen, solltet ihr euch auch darauf einstellen - allerdings weiss ich nicht ob das Informatik-Nebenfächler überhaupt betrifft, da ich nicht sicher bin ob wir überhaupt die 5 ECTS-Prüfung belegen dürfen.
Meinen Lösungsvorschlag habe ich auf einer seperaten Seite abgelegt, damit man nicht aus Versehen darüber liest: linkomopt2019-02-loesung
1) Flüsse
a) Maximalflussproblem mit Augmentierende-Wege-Algorithmus. Angeben des augmentierenden Wegs, Flusswertes und Zeichnen des Residualgraphen nach jedem Schritt. Zum Schluss Fluss und minimalen Schnitt angeben.
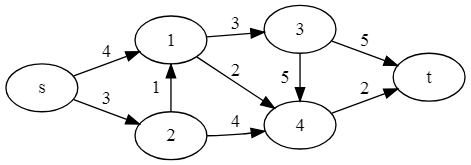
b) Minimalkosten-Flussproblem mit Kreislöschungs-Algorithmus. Angeben der Flusskosten, des negativen Kreises und Zeichnen des Residualgraphen nach jedem Schritt.
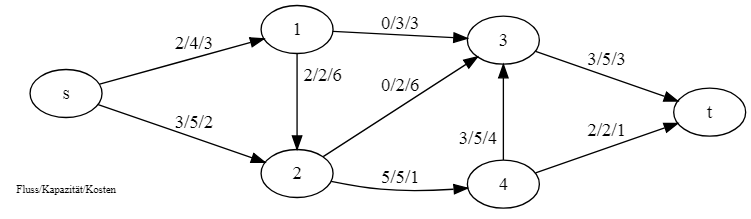
2) Modellierung
a) Einfaches Problem modellieren: Gesucht ist eine Futtermischung mit minimalen Kosten, die aber für drei Nährstoffe (N1, N2, N3) bestimmte Grenzen (in kg) einhält. Gegeben sind vier Grundstoffe (G1, G2, G3, G4), deren Nährstoffe (in kg) und Kosten pro Tonne. Zu Beginn benutze Variablen und deren Bedeutungen angeben.
| G1 | G2 | G3 | G4 | Mindestgrenze | Höchstgrenze | |
| N1 | 100 | 100 | 50 | 150 | 200 | 300 |
| N2 | 150 | 80 | 50 | 300 | 200 | — |
| N3 | 50 | 90 | 50 | 300 | 200 | — |
| Kosten | 400 | 200 | 300 | 1000 |
b) Duales Problem für das Problem aus a) aufstellen.
c) Zu beweisen: der optimale Zielfunktionswert beträgt 500. Den benötigten Satz angeben.
3) Simplex
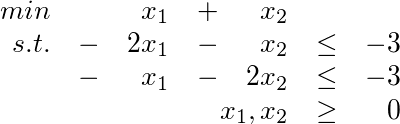
a) Zulässige Menge zeichnen. Optimallösung markieren.
Für die folgenden Aufgaben war die Standardform des Problems gegeben:
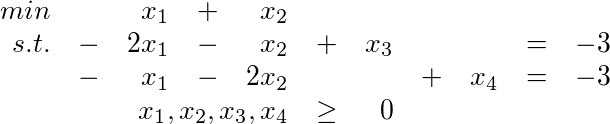
b) Primaler Simplex. Start mit B=(1,3), x_B = (3,3). Stoppt im Pricing der 2. Iteration.
c) Dualer Simplex. Start mit B = (1,4), z_N = (0.5,0.5). Stoppt im Pricing der 2. Iteration.
4) Graphen
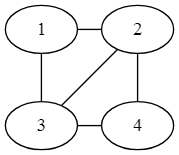
Gegeben ist ein einfacher, zusammenhängender Graph G=(V,E) (Bild oben). Ein Kantengraph K(G) = (V',E') mit V' = E, also jeder Knoten repräsentiert eine Kante aus G. Zwei Knoten in K(G) sind verbunden, wenn die entsprechenden Kanten in G einen gemeinsamen Endknoten haben.
a) K(G) für obiges G zeichnen.
b) Zu beweisen: Für jede Kante e = (v,w) in G gilt:
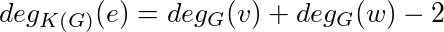
Folgendes Lemma darf für den Beweis verwendet werden: Wenn G einfach ist, ist auch K(G) einfach.
c) Zu beweisen: Wenn G eulersch ist, ist auch K(G) eulersch.
d) Zu begründen: Die Gegenrichtung von c) gilt im Allgemeinen nicht.
5) Verständnis
a) Dijkstra auf folgendem Graph ausführen. Distanzlabels und Vorgängerstruktur müssen erkennbar sein, und der besuchte Knoten soll markiert werden.
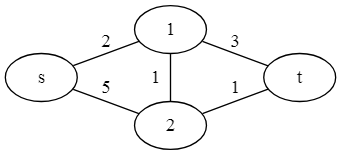
b) Zu begründen: das Minimalkostenflussproblem kann verwendet werden, um (i) das Kürzeste-Wege-Problem, (ii) das Maximalflussproblem zu berechnen.
c) Gegeben ist Graph G:
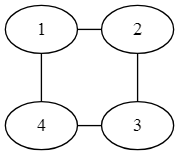
Basissystem und Kreissystem von M(G) sowie M*(G) angeben.
d) Wahr/Falsch-Fragen zum starken Dualitätssatz, ohne Begründung.
- Falls die Menge der zulässigen Lösungen für das primale Problem leer ist, ist das duale Problem unbeschränkt.
- Wenn das duale Problem eine endliche Optimallösung hat, hat auch das primale Problem eine endliche Optimallösung
- Wenn das duale Problem unbeschränkt ist, ist auch das primale Problem unbeschränkt.
- Wenn das primale Problem unbeschränkt ist, hat das duale Problem keine zulässige Lösung
