FSI Informatik/pruefungen/bachelor/aud/loesungws09

Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen (Übersicht)

Inhaltsverzeichnis

Forendiskussionen
Lösungsversuch

Forendiskussionen

Lösungsversuch

Aufgabe 1 - Wissensfragen

a) Richtig

b) [nicht mehr Stoff aktueller Semester]

O(n³)
O(√n)
O(√n*log2n)

d) 3. Antwort ist richtig

e) Falsch

f) Falsch

g) Bucketsort, Mergesort

h) Richtig, weil:

Zusammenhänge für die Höhe h eines AVL-Baums mit n Knoten:
log₂(n + 1) ≤ h < 1,441 * log₂(n + 2)

⇔ O(log₂(n + 1)) ≤ h < O(1,441 * log₂(n + 2))
⇔ O(log₂(n)) ≤ h < O(log₂(n + 2))
⇔ O(log₂(n)) ≤ h < O(log₂(n))

⇒ h ∈ O(log₂(n))

i) Falsch; nur bei gerader Anzahl an Elementen. Naja es hängt in v.a. auch von der Wahl des Pivot-Elementes ab.

j) O(1)

k) O(n)

Aufgabe 2 - Streutabellen

0	1	2	3	4	5	6	7
	3	6	1	12		2	5
			9	4

0	1	2	3	4	5	6	7
1₇	3₀	6₀	9₀	4₀	12₃	2₀	5₀

Die Anzahl der Buckets und die Schrittweite sollten teilerfremd sein, da sonst nicht alle Buckets abgedeckt werden können.
Ein Schlüssel kann so unter Umständen nicht der Hashtabelle hinzugefügt werden, obwohl noch Buckets frei wären.

Aufgabe 3 -Rekursion

a) kaskadenartige Rekursion

b) Die Implementierung ist ineffizient, weil viele Werte mehrfach berechnet werden.

private static long[][] b = new long[MAX][MAX];
// Vorinitialisierung des Felds b[][] mit -1
//Klausurfragestellung nicht ganz eindeutig, gefragt ist hier richtigerweise dynamische Programmierung mittels Memoization
 
private static long binom(int n, int k) { 
	if(k > n)
		return 0;
 
	if(k == 0 || k == n)
		return 1;
 
	if(b[n][k] == -1)
		b[n][k] = binom(n - 1, k - 1) + binom(n - 1, k);
 
	return b[n][k];
}

Aufgabe 4 - Suchbäume

Ein binärer Suchbaum ist ein total geordneter Baum, bei dem für jeden Knoten gilt:
Jeder Knoten des linken Teilbaums ist echt kleiner, jeder des rechten Teilbaums echt größer als der aktuelle Knoten.

Minimale Höhe ist O(log n)
Maximale Höhe ist O(n)

Gesucht ist vom aktuellen Knoten ausgehend das linkeste Kind des rechten Teilbaums Nicht der rechte Knoten von der Wurzel, sondern das linkeste Kind vom rechten Kind der Wurzel !

static int getNext(BinTree r) {
	// Annahme der Aufgabenstellung, dass es einen nächsten Wert gibt
	r = r.right;
 
	while(r.left != null) {
		r = r.left;
	}
 
	return r.value;
}

static boolean insert(BinTree b, int value) {
	BinTree prev = null;		// Schleppzeiger (kann nie null bleiben, solange der Baum nicht leer ist)
 
	while(b != null) {
		if(b.value == value)
			return false;
 
		if(b.value < value) {
			prev = b;
			b = b.right;
		} else {
			prev = b;
			b = b.left;
		}
	}
 
	if(prev.value < value) {
		prev.right = new BinTree(value);
	} else {
		prev.left = new BinTree(value);
	}
 
	return true;
}

oder rekursive Version:

static boolean insertRec(BinTree b, int value) {
        if (value > b.value) {
            if (b.right == null) {
                b.right = new BinTree(value);
                return true;
            }
            return insertRec(b.right, value);
        } else if (value < b.value) {
            if (b.left == null) {
                b.left = new BinTree(value);
                return true;
            }
            return insertRec(b.left, value);
        }
        return false;
    }

Aufgabe 5 - Halde

public static void haldenEigenschaftHerstellen(int[] feld) {
	for(int i = feld.length/2 - 1; i>= 0; i--) {
		versickern(feld, i, feld.length-1);
	}
}

O(n log n)

Sollte es nicht O(n) sein? In den VL-Folien steht, dass das Aufbauen einer Halde aus einem Array der Länge n nur O(n) ist. (Beweis wurde ausgelassen, aber intuitiv deswegen, weil die obere Hälfte des Arrays keine Kinder in der Halde hat ⇒ ein großer Teil fällt schon mal weg!)

Ja O(n), in der Klausur wurde nach der effizientesten Möglichkeit gesucht. Diese baut den Heap in O(n) auf, wie hier unter 4.2.4 beschrieben: http://linux-related.de/index.html?/coding/sort/sort_heap.htm

public static void haldenSortierung(int[] feld) {
	haldenEigenschaftHerstellen(feld);
 
	for(int i = 0; i < feld.length; i++) {
		tausche(feld, 0, feld.length - 1 - i);
 
		// Annahme, dass versickern nur mit validen "von" und "bis" Werte aufgerufen werden darf
		if(i < feld.length - 1)
			versickern(feld, 0, feld.length - 2 - i);
	}
}

Das ginge meines Erachtens (bei anderer Angabe noch leichter), oder??:

public static void haldenSortierung(int[] feld){
    haldenEigenschaftHerstellen(feld);
 
    for(int i = feld.length - 1; i > 0; i--){
        tausche(feld, 0, i);
        versickern(feld, 0, i - 1);
    }
}

Programm zum selbst Testen:
:pruefungen:bachelor:aud:heapsort.java.txt

versickern: O(log n)
haldenSortierung: O(n log n)

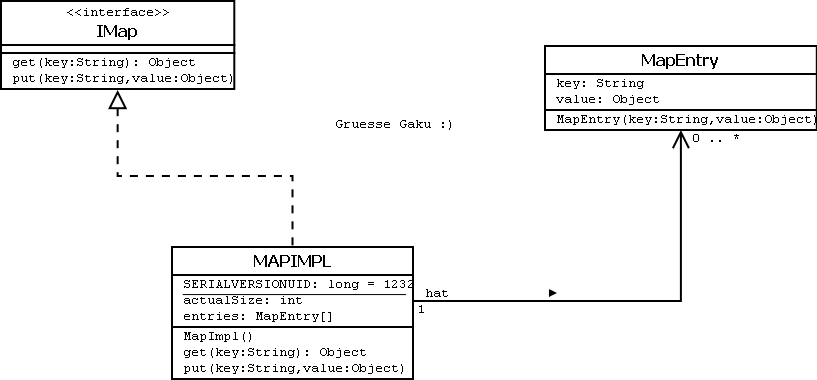
Aufgabe 6 - UML

Aufgabe 7 - Graphen

a) Adjazenzmatrix

	A	B	C	D
A	-	4	2	-
B	4	-	1	-
C	2	1	-	5
D	-	-	5	-

b) Dijkstra

A	B	C	D	E	F	G	H
[0]	∞	∞	∞	∞	∞	∞	∞
	4_A	[2_A]	∞	∞	∞	∞	∞
	[3_C]		7_C	∞	∞	∞	∞
			7_C	∞	[4_B]	∞	∞
			7_C	[5_F]		∞	8_F
			[7_C]			10_E	8_F
						10_E	[8_F]
						[9_H]

[9_H] → [8_F] → [4_B] → [3_C] → [2_A] → [0]

⇒ A → C → B → F → H → G

c) Euler

Eine von mehreren Möglichkeiten:

Welche Kanten werden vom Algorithmus als nächstes in Betracht gezogen?
EG, HF, BA, CA, DC

Welche dieser Kanten fugt der Algorithmus im nächsten Schritt der Lösungsmenge hinzu? \\CA

Die Kante DC wird nicht genommen, da nur Kanten hinzugefügt werden, die zu einem noch nicht besuchten Knoten führen.

Aufgabe 8 – Abstrakte Datentypen

contains(x, create) = false
contains(x, put(x, M)) = true
contains(x, put(y, M)) = contains(x, M);

oder

axs
contains(s, create()) = FALSE
contains(s, put(a, m)) = { TRUE             falls s = a
                         { contains(s, m)   sonst

count:	String x MultiSet   ->   Integer

count(x, create) = 0
count(x, put(x, M)) = 1 + count(x, M)
count(x, put(y, M)) = count(x, M)

oder

ops
count:	String x MultiSet   ->   Integer

axs
count(s, create()) = 0
count(s, put(a, m)) = { 1 + count(s, m)  falls s = a
                      { count(s, m)      sonst

purge:	String x MultiSet   ->   MultiSet

purge(x, create) = create
purge(x, put(x, M)) = purge(x, M)
purge(x, put(y, M)) = put(y, purge(x, M))

oder

ops
purge:	String x MultiSet   ->   MultiSet

axs
purge(s, create()) = create()
purge(s, put(a, m)) = { purge(s, m)            falls s = a
                      { put(a, purge(s, m))    sonst

Primärkonstruktoren:
create, put

Aufgabe 9 - wp-Kalkül

wp("a = a*3 - 1; b = 80 - a; b--;", b > 47) =
wp("a = a*3 - 1; b = 80 - a; b = b - 1;", b > 47) =
wp("a = a*3 - 1; b = 80 - a;", b - 1 > 47) =
wp("a = a*3 - 1;", 80 - a - 1 > 47) =
(80 - (a*3 - 1) - 1 > 47) =
(80 - a*3 + 1 - 1 > 47) =
(33 > a*3) =
(11  > a)

wp("if (x < 0 || x > 7) {x = 7 - x;} else {x = 8 + x;}", x != 7) = 
[(x < 0 ∨ x > 7) ∧ wp("x = 7 - x;", x != 7)] ∨ [¬(x < 0 ∨ x > 7) ∧ wp("x = 8 + x;", x != 7)] = 
[(x < 0 ∨ x > 7) ∧ (7 - x != 7)] ∨ [(x ≥ 0) ∧ (x ≤ 7) ∧ (8 + x != 7)] = 
[(x < 0 ∨ x > 7) ∧ (x != 0)] ∨ [(x ≥ 0) ∧ (x ≤ 7) ∧ (x != -1)] = 

(x != 0) ist durch (x < 0 ∨ x > 7) schon abgedeckt
(x != -1) ist durch (x ≥ 0) ∧ (x ≤ 7) schon abgedeckt

(x < 0) ∨ (x > 7) ∨ ((x ≥ 0) ∧ (x ≤ 7)) = 
(x < 0) ∨ (x > 7) ∨ (0 ≤ x ≤ 7) = 
(true)

LO: falsch
	a = 1, i = n
	mf(n, i) = mf(n, n) = 0

RO: falsch
	a = 1, i = n
	mf(n, k) - mf(i, k) = mf(n, k) - mf(n, k) = 0

LU: korrekt
	a = 1, i = n
	(mf(n, k) / (mf(i, k) = (mf(n, k) / (mf(n, k) = 1
	
RU: falsch
	a = 1, i = n
	mf(n, i) - mf(k, i) = mf(n, n) - mf(k, n) = 0 - mf(k, n) = -mf(k, n) < 0

ii)

Zu zeigen: {I ∧ b} = wp(A, I)

wp(A, I) = 
wp("a = a*i; i = i - k;", a = (mf(n, k)) / (mf(i, k)) ) = 
wp("a = a*i;", a = (mf(n, k)) / (mf(i - k, k)) ) = 
(a*i = (mf(n, k)) / (mf(i - k, k)) ) = 
(a = (mf(n, k)) / (mf(i - k, k) * i) ) = 
= (*) = (a = (mf(n, k)) / (mf(i, k)) )

(*) Nebenrechnung:
mf(i - k, k) = (i - k) * (i - 2k) * (i - 3k) * ... * 1
mf(i - k, k) * i = (i - k) * (i - 2k) * (i - 3k) * ... * 1 * i
und das entspricht
mf(i, k) * i = i* (i - k) * (i - 2k) * (i - 3k) * ... * 1

{I ∧ b} => wp(A, I)
{a = (mf(n, k)) / (mf(i, k)) ∧ i > 0)} => (a = (mf(n, k)) / (mf(i, k)) )
trivial, da die schwächste Vorbedingung nur restriktiver gemacht wurde

iii)

V = i
i = n, n > 0	-> V > 0 zu Beginn
i = i - k, k > 0	-> i ist monoton fallend