Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » aud » Forendiskussionen (Übersicht)
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Aufgabe 1 - Wissensfragen
a) O(n²)
b) Falsch, bei einer abstrakten Klasse ist dies nicht notwendig
c)
- Bubblesort: in-place, stabil
- Mergesort: stabil
- Quicksort: in-place
d) 1., 3. und 6. Antwort sind richtig
e) Richtig
f) 2. und 3. Antwort sind richtig (RuntimeException oder Unterklassen oder Error oder Unterklassen müssen nicht deklariert werden.)
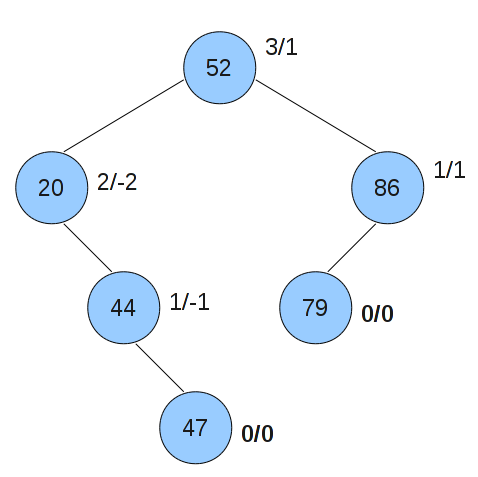
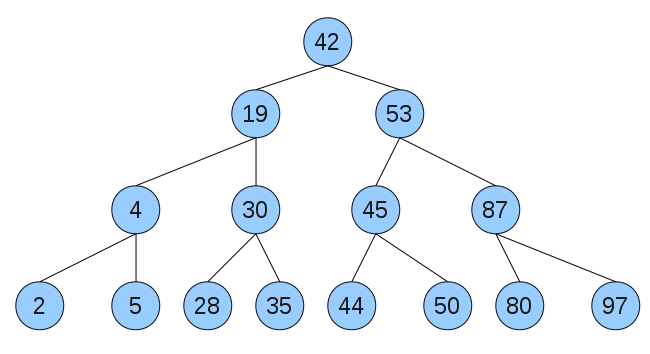
Aufgabe 2 - AVL-Bäume
a)
Nein, der Baum ist kein AVL-Baum, da sich die Teilbäume in ihrer Höhe um mehr als 1 unterscheiden.
b)
21
/ \
5 95
/ \
4 10
c)
d)
Es muss eine Doppelrotation ausgeführt werden: einmal gegen, dann im Uhrzeigersinn.
42
/ \
23 50
/ \ \
5 37 69
(Der Balancefaktor bei 69 ist 0. 0 passt sowohl zu positivem als auch negativem Vorzeichen, folglich würde hier auch eine Einfachrotation reichen.)
e)
- Auffinden des zu löschenden Elements: O(log n)
- Auffinden des größten Elements des linken Teilbaums, sollte der zu löschende Knoten Kinder haben: O(log n)
- Löschen des Knotens bzw. überschreiben seines Wertes mit dem gefundenen Nachfolger-Knoten: O(1)
- Mögliche Änderungsstellen des AVL-Baums sind auf dem Pfad bis zur Wurzel: O(log n)
- Jegliche Rotation: O(1)
Insgesamt ergibt sich somit ein Aufwand von O(log n)
Aufgabe 3 - Schreibtischlauf
Java Datei zum selbst testen: :pruefungen:bachelor:aud:walkthrough.java.txt
- : d a a
- : [d, d, d, d] [a, b, c, d]
- : [a, d, c, d] [a, b, a, d]
Aufgabe 4 - Streuspeicherung
a)
(-) Werte nicht gleich verteilt (-) Lastfaktor nicht optimal (+) Tabelle ist auf jeden Fall teilerfremd mit Schrittweite, da Länge (13) eine Primzahl ist
b)
i)
| 0 | (0,0) → (2,1) |
|---|---|
| 1 | (2,3) |
| 2 | |
| 3 | (0,6) |
| 4 | (3,3) |
| 5 | (3,5) → (1,4) → (5,6) |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | (2,8) |
| 11 | |
| 12 |
ii)
Die Hashfunktion müsst so gewählt sein, dass für jede Eingabe derselbe Bucket errechnet wird. Dies geht beliebig einfach oder kompliziert.
Einfachstes Beispiel: h(x_1, x_2) = 0
iii)
O(n), da nun alle Werte in einer einzigen Liste verkettet sind
c)
i)
| 0 | (0,0) |
|---|---|
| 1 | (2,3) |
| 2 | |
| 3 | (2,1)* |
| 4 | (3,3) |
| 5 | (3,5) |
| 6 | (0,6)* |
| 7 | |
| 8 | (1,4)* |
| 9 | |
| 10 | (2,8) |
| 11 | (5,6)* |
| 12 |
ii)
Lastfaktor = 9/13 = 0,69
Aufgabe 5 - Sortieren
a)
i)
BubbleSort
ii)
Sie muss komplett aufsteigend sortiert sein.
iii)
Sie muss komplett absteigend sortiert sein.
iv)
Zeile 6:
for(int i = 0; i < n − 1 - j; ++i) {
Beobachtung beim BubbleSort Verfahren:
Nach jedem vollständigen Abarbeiten der inneren Schleife steht (mindestens) ein weiteres Element, nämlich das größte, das bisher noch nicht an seiner endgültigen Position stand, an eben jener.
Am Beispiel:
{3,2,1} → {2,3,1} → {2,1,3}
Zumindest Element 3 steht nun an seiner finalen Position.
Man kann somit Schritt für Schritt die hintere Grenze für die innere Schleife dekrementieren.
Programm zum selbst testen: :pruefungen:bachelor:aud:bubblesort.java.txt
b)
| T | 4 8 1 5 | 7 2 6 3 | ||||||
|---|---|---|---|---|---|---|---|---|
| T | 4 8 | 1 5 | 7 2 6 3 | |||||
| T | 4 | 8 | 1 5 | 7 2 6 3 | ||||
| M | 4 8 | 1 5 | 7 2 6 3 | |||||
| T | 4 8 | 1 | 5 | 7 2 6 3 | ||||
| M | 4 8 | 1 5 | 7 2 6 3 | |||||
| M | 1 4 5 8 | 7 2 6 3 | ||||||
| T | 1 4 5 8 | 7 2 | 6 3 | |||||
| T | 1 4 5 8 | 7 | 2 | 6 3 | ||||
| M | 1 4 5 8 | 2 7 | 6 3 | |||||
| T | 1 4 5 8 | 2 7 | 6 | 3 | ||||
| M | 1 4 5 8 | 2 7 | 3 6 | |||||
| M | 1 4 5 8 | 2 3 6 7 | ||||||
| M | 1 2 3 4 5 6 7 8 | |||||||
c)
public static int[] mergesort(int[] m) { if(m.length <= 1) return m; int nLeft = m.length / 2; int nRight = m.length - nLeft; int[] left = new int[nLeft]; int[] right = new int[nRight]; for(int i = 0; i < nLeft; ++i) { left[i] = m[i]; } for(int i = 0; i < nRight; ++i) { right[i] = m[nLeft + i]; } return merge(mergesort(left), mergesort(right)); }
public static int[] merge(int[] left, int[] right) { int[] result = new int[left.length + right.length]; int i = 0; int j = 0; int k = 0; while(i < left.length && j < right.length) { if(left[i] <= right[j]) { result[k] = left[i++]; } else { result[k] = right[j++]; } ++k; } while(i < left.length) { result[k] = left[i]; ++i; ++k; } while(j < right.length) { result[k] = right[j]; ++j; ++k; } return result; }
Programmcode zum selber testen: :pruefungen:bachelor:aud:mergesort.java.txt
Aufgabe 6 - Graphen
a)
| Ingolstadt | Hof | Würzburg | Nürnberg | Regensburg | AK Deggendorf | AD Holledau | Passau | München |
|---|---|---|---|---|---|---|---|---|
| [0] | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| 0 | ∞ | ∞ | 90 | ∞ | ∞ | [20] | ∞ | ∞ |
| 0 | ∞ | ∞ | 90 | 90 | ∞ | 20 | ∞ | [70] |
| 0 | ∞ | ∞ | [90] | 90 | 210 | 20 | ∞ | 70 |
| 0 | 225 | 205 | 90 | [90] | 210 | 20 | ∞ | 70 |
| 0 | 225 | 205 | 90 | 90 | [160] | 20 | ∞ | 70 |
| 0 | 225 | [205] | 90 | 90 | 160 | 20 | 210 | 70 |
| 0 | 225 | 205 | 90 | 90 | 160 | 20 | [210] | 70 |
| 0 | [225] | 205 | 90 | 90 | 160 | 20 | 210 | 70 |
| Ergebnis: | 225 | 205 | 90 | 90 | 160 | 20 | 210 | 70 |
b)
| von | nach |
|---|---|
| Ingolstadt | AD Holledau |
| AD Holledau | München |
| AK Deggendorf | Passau |
| AD Holledau | Regensburg |
| Regensburg | AK Deggendorf |
| Ingolstadt | Nürnberg |
| Nürnberg | Würzburg |
| Nürnberg | Hof |
Es sind auch leichte Abwandlungen hiervon gültig.
c)
(Scheinbar nicht mehr Stoff aktueller Semester)
Ein Euler-Pfad ist ein Pfad, der jede Kante exakt einmal enthält. Mögliche Lösung: AD Holledau ↔ Passau
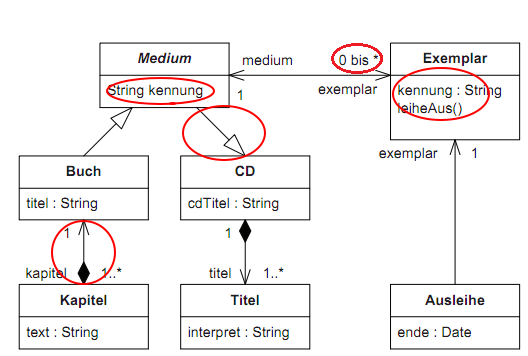
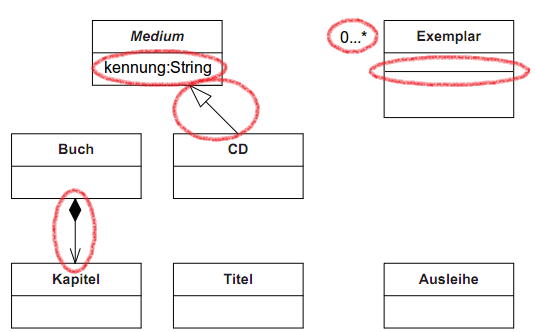
Aufgabe 7 - UML
Aufgabe 8 - Rekursion und Iteration
a)
Kaskadenartige Rekursion, da mehrere rekursive Aufrufe im Rumpf vorkommen.(auf Schleife achten)
b)
Es werden keine Zwischenwerte gespeichert und somit immer wieder identische Zwischenergebnisse mehrfach berechnet.
c)
private static int [ ] maxKnown = new int [MAX] ; // Gehen Sie davon aus , dass alle maxKnown [i] vorab mit −1 // korrekt initialisiert wurden. private static int knapsack (Item [ ] items , int capacity) { if(maxKnown[capacity]!= -1) { return maxKnown[capacity]; } int maxValue = 0 ; for (int i = 0 ; i < items . length ; ++i ) { int spaceLeft = capacity − items [i].size; if(spaceLeft >= 0 ) { int value = knapsack(items, spaceLeft) + items[i].value; if(value > maxValue) { maxValue = value; } } } maxKnown[capacity] = maxValue; return maxValue; }
Aufgabe 9 - wp-Kalkül
a)
wp("if (a ≤ b) {a = -(2*b + a); b -= 1 - a;} else {b = -b - a - 1;}", b < 0) =
[(a ≤ b) ∧ wp("a = -(2*b + a); b = b - (1 - a);" b < 0)] ∨ [¬(a ≤ b) ∧ wp("b = -b - a - 1", b < 0)] =
[(a ≤ b) ∧ wp("a = -(2*b + a);" b - (1 - a) < 0)] ∨ [(a > b) ∧ (-b - a - 1 < 0)] =
[(a ≤ b) ∧ (b - (1 - (-(2*b + a))) < 0)] ∨ [(a > b) ∧ (-b - a - 1 < 0)] =
[(a ≤ b) ∧ (b -1 -2*b - a < 0)] ∨ [(a > b) ∧ (-b - a - 1 < 0)] =
[(a ≤ b) ∧ (-b - a - 1 < 0)] ∨ [(a > b) ∧ (-b - a - 1 < 0)] =
(-b - a - 1 < 0)
b) i)
**LO:** Falsch, schon vor der Schleife ungültig: k = 1, kf = 1, kfs = 1 kfs = kf! - 1 1 = 1 - 1 1 = 0 **RO:** Richtig, Summe wird bis zum momentanen k gebildet **LU:** Falsch, schon vor der Schleife ungültig: k = 1, kf = 1, kfs = 1 kf = kfs + k! 1 = 1 + 1! 1 = 2 **RU:** Falsch, es wird bis n-1 summiert, egal wie oft die schleife durchlaufen wird Alternativ: Schon vor der Schleife ungültig: k = 1, kf = 1, kfs = 1 ... ∧ kf = (k + 1)! ∧ ... ... ∧ 1 = (1 + 1)! ∧ ... ... ∧ 1 = 2 ∧ ...
b) ii)
Zu zeigen: (I ∧ b) => wp(A,I)
wp("kf *= k; kfs += kf; k++;", kfs = ∑ i! ∧ kf = (k-1)! ∧ 1 <= k <= n) =
wp("kf = kf * k; kfs = kfs + kf; k = k + 1;", kfs = ∑ i! ∧ kf = (k-1)! ∧ 1 <= k <= n) =
wp("kf = kf * k; kfs = kfs + kf;", kfs = ∑ i! ∧ kf = (k + 1-1)! ∧ 1 <= k + 1 <= n) =
wp("kf = kf * k;", kfs + kf = ∑ i! ∧ kf = (k + 1 - 1)! ∧ 1 <= k + 1 <= n) =
(kfs + kf * k = ∑ i! ∧ kf * k = (k + 1 - 1)! ∧ 1 <= k + 1 <= n) =
(kfs = ∑ i! - kf * k ∧ kf = (k - 1)! ∧ 0 <= k <= n - 1)
{I ∧ b} => wp(A,I) =
{(kfs = ∑ i! ∧ kf = (k-1)! ∧ 1 <= k <= n) ∧ k ≤ n - 1} => (kfs = ∑ i! - kf * k ∧ kf = (k - 1)! ∧ 0 <= k <= n - 1) =
¬(kfs = ∑ i!) ∨ ¬(kf = (k-1)!) ∨ ¬(1 <= k <= n) ∨ ¬(k ≤ n - 1) ∨ (kfs = ∑ i! - kf * k ∧ kf = (k - 1)! ∧ 0 <= k <= n - 1) =
(kfs ≠ ∑ i!) ∨ (kf ≠ (k-1)!) ∨ (n < k < 1) ∨ (k > n - 1) ∨ (kfs = ∑ i! - kf * k ∧ kf = (k - 1)! ∧ 0 <= k <= n - 1) =
...
b) ii) V = (n - 1) - k
k wird sukzessive erhöht, während (n-1) von der Eingabe abhängig, aber im Programm selbst konstant ist. V ist damit monoton fallend. Durch die Abbruchbedingung der Schleife ist V nach unten durch die 0 beschränkt.