Du befindest dich hier: FSI Informatik » Prüfungsfragen und Altklausuren » Prüfungen im Bachelor-Studium (1. - 5. Semester) » algoks » Forendiskussionen (Übersicht)
Inhaltsverzeichnis
Forendiskussionen
Lösungsversuch
Lösungen ohne gewähr, da irgendwann zwischen 11 und 1 Uhr und 6-7 Uhr vor der Klausur schnell gemacht (ja abends, und morgens). Ich klatsche es nur hier hin, fuer die naechste Generation. Viel Spaß bei der Klausur 
Aufgabe 1 - Komplexität
- a)
a) O(n)
b) O(n³)
c) O(n^2)
d) O(n log n)
e) 1
f) 2
g) O(h²)
h) O(h^4)
- b)
nein, nein, ja, ja
Aufgabe 2 - Lösen linearer Gleichungsszsteme
a) Erste iteration:
R_1 = |2 1 3|
|0 1 -2|
|0 3 -4|
Lösung:
R = |2 1 3|
|0 1 -2|
|0 0 2|
L = |1 0 0|
|2 1 0|
|-2 3 1|
b)
x = |-3|
|3|
|2|
c)
x_1 = |8|
|0|
|0|
|8|
x_2 = |8|
|-4|
|-4|
|8|
d)
x_1 = | 8|
|-4|
| 2|
| 7|
e) Theoretisch exakt, praktisch wegen Rundungsfehlern oft als iteratives Verfahren angewendet.
Aufgabe 3 - Speicherung dünn besetzter Matrizen
a)
val 2 3 -4 7 3 2 2 -1 row_ind 2 3 4 1 2 3 1 3 col_ptr 0 0 3 6 6 8
b)
Speicherung erfolgt im CRS-Format. Hierzu muss nur row_ind als col_ind bzw. col_ptr als row_ptr interpretiert/kopiert werden.
c)
| 0 4 0 0 | | 0 0 0 0 | | 0 0 3 8 | | 0 2 -1 4 | | 0 0 0 0 |
Aufgabe 4 - Falten und Filtern
a)
ja (1 2 1)^T (1 2 1)
nein
ja (1 2 3)^T (-1 0 1)
b)
5^2 * (N-4)^2
c)
2*5*(N-4)^2
d)
double getValue (const unsigned int& x, const unsigned int& y) const {
return data.at(2 * x + y);
}
e)
void setValue (const unsigned int& x, const unsigned int& y, double value) {
data.at(2 * x + y) = value;
}
f)
filter
{
double filter[3][3] =
{
{0,1,0},
{1,-4,1},
{0,1,0}
};
for(int x=1;x<src.getDim()-1; x++)
{
for(int y=1;y<src.getDim()-1; y++)
{
double newValue=0;
for(int i=0;i<3;i++)
{
for(int j=0;j<3;j++)
{
newValue+=src.getValue(x-1+i,y-1+j)*filter[j][i];
}
}
dest.setValue(x-1,y-1,newValue);
}
}
}
g)
filter
{
Image tmp(src.getDim());
double filterX[3]={3,10,3};
double filterY[3]={1,0,-1};
for(int x=0;x<src.getDim();x++)
{
for(int y=1;y<src.getDim()-1;y++)
{
double newValue=0;
for(int i=0;i<3;i++)
{
newValue+=src.getValue(x,y-1+i)*filterY[i];
}
tmp.setValue(x,y-1,newValue);
}
}
for(int x=1;x<src.getDim()-1;x++)
{
for(int y=1;y<src.getDim()-1;y++)
{
double newValue=0;
for(int i=0;i<3;i++)
{
newValue+=src.getValue(x-1,y-1+i)*filterX[i];
}
tmp.setValue(x-1,y-1,newValue);
}
}
}
Aufgabe 5 - Interpolation
a)
y-Werte = 1, -1, 1, 2
von-nach: 0–0.5, 0,5–1,5, 1,5–3, 3–4(,5)
b)
| -2x+1 < 2x-3 | 1/2x
c)
m_1 = 0
m_2 = 3/2
d)
e)
f_p = 8
f)
rho = 1/4
sigma = 1/2
tau = 1/4
f_p = 6
Aufgabe 6 - Bezier-Kurven
meine Sexistische Bildbeschreibung
a)
Schaut wie ein Busen (von oben) aus. :)
b)
Busen der links und rechts ausbuechst :)
Ist leider falsch, da das die Eigenschaft „BK liegt in der konvexen Huelle des Kontrollpolygons“ verletzt. Mein Vorschlag waere, an den beiden Eckpunkten nicht tangetial nach innen zu laufen.
c)
„Brustbein“ ist unterhalb des mitleren zackens
d)
Lösungsansatz: i have no idea what i am doing here Zuerst die Ecken:
c_0 = kp[0]; d_(kp.dim-1) =kp[kp.dim -1
Dann den rest mit dem Code aus der Vorlesung (oder Script)
for(k = 1, ....){
for(i...){
}
Vor ende der aeusseren For-Schleife die interesanten Werte uebernehmen:
c_k = kp_k d_kp.dim -k = kp_kp.dim-k }
Ggf. Arbeitskopie von kp machen, off by one Fehler
Aufgabe 7 - Singulaerwertzerlegung
a)
Singulaerwerte: 6, 3, 3
Rang: 3
Bildraum: <1/9(1 4 8)^T,1/9(4 7 -4)^T, 1/9(8 -4 1)^T>
Kern: <1/2 (-1 1 1 1)^T
Konditionszahl: 2
b)
| 5 | | -11 | | 9 | | 7 |
c)
Formel siehe hier fuer Erklaerung.
A_1 = u_1 * sigma_1 * v1^T
A_1 =
1/3 * | 1 1 1 -1 |
| 4 4 4 -4 |
| 8 8 8 -8 |
Aufgabe 8 - Nichtlineare Optimierung
a)
x_1 = (9/8 3) ^T
s_0 = (1 0) —> ist bei der Aufgabe aber gar nicht gefragt, bzw. wird nicht benoetigt.
b)
maxIter ||x_i+1 - x_i|| < epsilon ||F(x_i)|| < epsilon (Nullstellensuche)
c)
x^1 = (1 3)
d)
Vorgehensweise: Y = b^T * A berechnen; Danach Y * (x_1, x_2)^T =! 0
Y = (0, 4)^T
Es muss folgendes LGS geloest werden: 0 * x_1 + 4 * x_2 = 0
(1 0)^T —> x_1 kann beliebig gewaehlt werden.
e)
[5/4,13/4] T
Es gibt keine Aufgabe 8e)
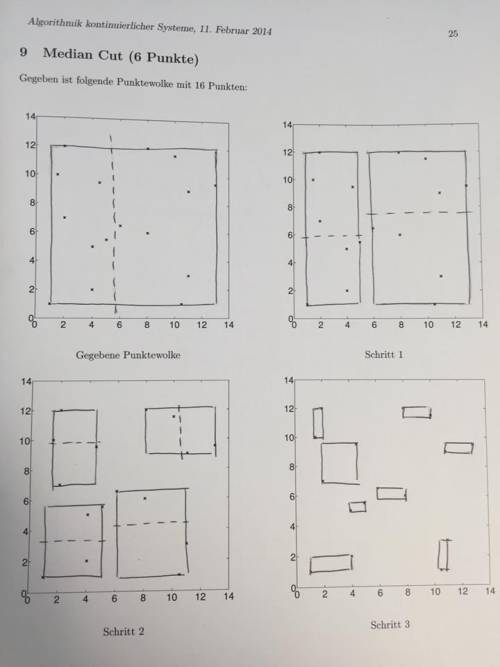
Aufgabe 9 - Median Cut
Median Cut konnte ich aus den Vorlesungsfolien nicht nachvollziehen.
1. Bounding Box zeichnen: Ein Rechteck zeichnen, bei dem alle Punkte innerhalb der Box liegen. Die aeussersten Punkte markieren dabei die Grenzen des Rechtecks.
2. Bounding Box halbieren, dass in etwa gleich viele Punkte in der oberen/linken und unteren/rechten Box liegen.
3. Das wird rekursiv fuer jede weitere Box gemacht (hier 3x, da nur 3 Schritter verlangt sind).